题目内容
11.设A为不等式log2(5x2-8x+3)>2的解集,B为不等式2${\;}^{{x}^{2}-2x-k}$≥$\frac{1}{2}$的解集.(1)求集合A,B;
(2)如果A⊆B,求实数k的取值范围.
分析 (1)根据指数函数和对数函数的单调性,可将原不等式转化为整式不等式,解得A,B;
(2)根据(1)中结论,分类讨论满足A⊆B的实数k的取值范围,综合讨论结果,可得答案.
解答 解:(1)若log2(5x2-8x+3)>2,则5x2-8x+3>4,即5x2-8x-1>0,
解得:A=(-∞,$\frac{4-\sqrt{21}}{5}$)∪($\frac{4+\sqrt{21}}{5}$,+∞);
若2${\;}^{{x}^{2}-2x-k}$≥$\frac{1}{2}$,则x2-2x-k≥-1,即x2-2x+1-k≥0,
当k≤0时,B=R;
当k>0时,B=(-∞,1-$\sqrt{k}$]∪[1+$\sqrt{k}$,+∞);
(2)当k≤0时,B=R,满足A⊆B,
当k>0时,B=(-∞,1-$\sqrt{k}$]∪[1+$\sqrt{k}$,+∞),由A⊆B得:$\left\{\begin{array}{l}1-\sqrt{k}≥\frac{4-\sqrt{21}}{5}\\ 1+\sqrt{k}≤\frac{4+\sqrt{21}}{5}\end{array}\right.$
解得:0<k≤$\frac{22-2\sqrt{21}}{25}$,
故k≤$\frac{22-2\sqrt{21}}{25}$.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
16.“lgx,lgy,lgz成等差数列”是“y2=xz”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.已知点A(5,0),抛物线C:y2=4x的焦点为F,点P在抛物线C上,若点F恰好在PA的垂直平分线上,则PA的长度为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
16.圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
| A. | $\frac{\sqrt{7}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{2}{5}\sqrt{7}$ | D. | $\sqrt{7}$ |
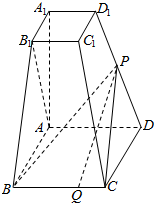 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.