题目内容
(本题满分14分)如图, 在直三棱柱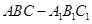 中,
中,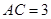 ,
,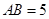 ,
,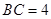
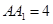 ,点
,点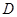 是
是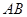 的中点.
的中点.
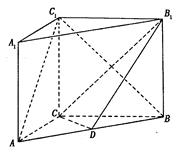
⑴求证: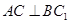 ;
;
⑵求证: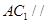 平面
平面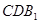 ;
;
⑶求二面角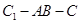 的正切值.
的正切值.
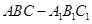 中,
中,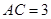 ,
,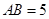 ,
,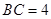
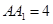 ,点
,点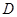 是
是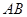 的中点.
的中点.
⑴求证:
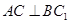 ;
;⑵求证:
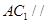 平面
平面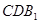 ;
;⑶求二面角
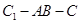 的正切值.
的正切值.⑴见解析;⑵见解析;⑶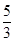
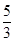
本试题主要考查了立体几何中的线线垂直的证明,以及线面平行的判定和二面角的平面角的求解的综合运用。
(1)由于已知中三棱柱的性质和三角形可知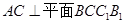 ,得到结论。
,得到结论。
(2)利用线线平行来判定得到线面平行的证明。
(3)由于二面角的平面角可以建立空间直角坐标系,求解平面的法向量来表示夹角得到二面角 平面角的求解。
证明:⑴、在直三棱柱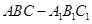 ,
,
∵底面三边长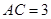 ,
,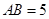 ,
,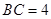 ,∴
,∴ 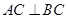 ,………1分
,………1分
又直三棱柱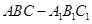 中,
中,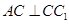 ,且
,且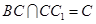 ,
,
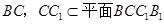 ,∴
,∴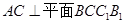 .……………3分
.……………3分
而 ,∴
,∴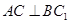 ;…………………………4分
;…………………………4分
⑵、设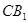 与
与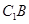 的交点为
的交点为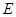 ,连结
,连结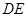 ,…5分
,…5分
∵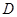 是
是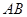 的中点,
的中点,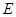 是
是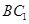 的中点,∴
的中点,∴ 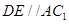 ,………7分
,………7分
∵ ,
,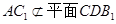 ,∴
,∴ .…8分
.…8分
⑶、过点C作CF⊥AB于F,连接C1F.…………9分
由已知C1C垂直平面ABC,
则∠C1FC为二面角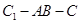 的平面角。………11分
的平面角。………11分
在Rt△ABC中,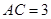 ,
,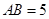 ,
,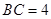 ,则
,则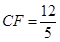 …………12分
…………12分
又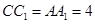 ,∴
,∴ 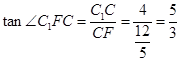 ,……………13分
,……………13分
∴二面角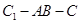 的正切值为
的正切值为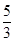 .…………………………14分
.…………………………14分
(另:可以建立空间直角坐标系用向量方法完成,酌情给分,过程略)
(1)由于已知中三棱柱的性质和三角形可知
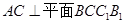 ,得到结论。
,得到结论。(2)利用线线平行来判定得到线面平行的证明。
(3)由于二面角的平面角可以建立空间直角坐标系,求解平面的法向量来表示夹角得到二面角 平面角的求解。
证明:⑴、在直三棱柱
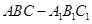 ,
,∵底面三边长
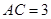 ,
,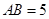 ,
,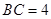 ,∴
,∴ 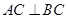 ,………1分
,………1分又直三棱柱
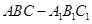 中,
中,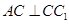 ,且
,且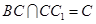 ,
,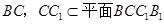 ,∴
,∴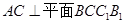 .……………3分
.……………3分而
 ,∴
,∴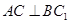 ;…………………………4分
;…………………………4分⑵、设
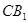 与
与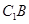 的交点为
的交点为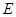 ,连结
,连结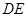 ,…5分
,…5分∵
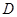 是
是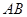 的中点,
的中点,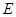 是
是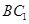 的中点,∴
的中点,∴ 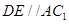 ,………7分
,………7分∵
 ,
,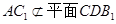 ,∴
,∴ .…8分
.…8分⑶、过点C作CF⊥AB于F,连接C1F.…………9分
由已知C1C垂直平面ABC,
则∠C1FC为二面角
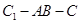 的平面角。………11分
的平面角。………11分在Rt△ABC中,
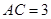 ,
,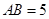 ,
,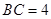 ,则
,则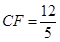 …………12分
…………12分又
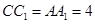 ,∴
,∴ 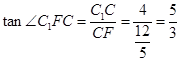 ,……………13分
,……………13分∴二面角
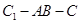 的正切值为
的正切值为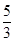 .…………………………14分
.…………………………14分(另:可以建立空间直角坐标系用向量方法完成,酌情给分,过程略)

练习册系列答案
相关题目
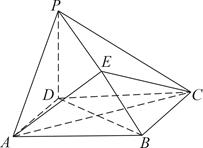
 AB且E为PB的中点时,求AE与平面PDB所成角的大小。
AB且E为PB的中点时,求AE与平面PDB所成角的大小。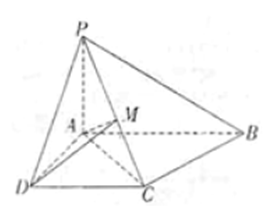
 中,
中, 平面
平面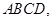 四边形
四边形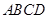 为正方形,
为正方形,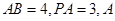 点在
点在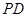 上的射影为
上的射影为 点.
点.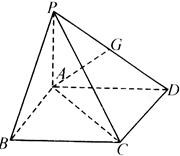
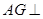 平面
平面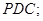
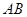 上是否存在一点
上是否存在一点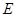 ,使得
,使得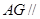 平面
平面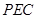 .若存在,求出
.若存在,求出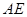 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.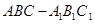 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则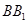 与平面
与平面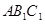 所成的角的大小为
所成的角的大小为 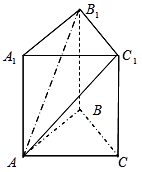
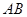 是圆
是圆 的直径,
的直径,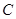 是异于
是异于 ,
, 两点的圆周上的任意一点,
两点的圆周上的任意一点, 垂直于圆
垂直于圆 ,
,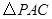 ,
,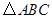 ,
,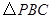 中,直角三角形的个数是( )
中,直角三角形的个数是( )
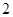
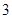
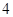

 、
、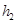 、
、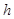 ,则
,则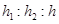 等于( )
等于( )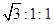

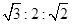

 表示平面,则以下命题正确的有( )
表示平面,则以下命题正确的有( ) ; ②
; ② ; ③
; ③ ; ④
; ④ .
.