题目内容
3.已知命题p:“直线l垂直于平面α内的无数条直线”的充要条件是“l⊥α”;命题q:若平面α⊥平面β,直线a?β,则“a⊥α”是“a平行于β”的充分不必要条件,则正确命题是( )| A. | p∧q | B. | (¬p)∧q | C. | (?p)∧(¬q) | D. | p∨(¬q) |
分析 别判断命题,p,q的真假,然后利用复合命题之间的关系即可得到结论.
解答 解:对于命题p:直线l垂直于平面α内的无数条直线,这些直线可能是一组平行线,若是此种情况,由线面垂直的定义知,不能得出l⊥α,
由l⊥α知,线与面内的每一条直线都是垂直的,故可得出直线l垂直于平面α内的无数条直线,
由上证明知“直线l垂直于平面α内的无数条直线”是“l⊥α”必要不充分条件,
故p是假命题;
对于命题q:若平面α⊥平面β,直线a?β,则当a⊥α时,有a∥β成立,
当a∥β时,a⊥α或a与α相交,∴a⊥α不一定成立,即“a⊥α”是“a∥β”的充分不必要条件,
∴q为真命题;
则¬p∧q为真命题,
故选:B.
点评 本题主要考查复合命题之间的关系,利用线面垂直和平行的性质和判定定理是解决本题的关键.

练习册系列答案
相关题目
10.若(x-i)i=y+2i,x,y∈R,则复数x+yi在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
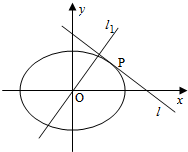 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.