题目内容

4、已知抛物线y2=4ax的准线与圆x2+y2-2y=0相离，则实数a的取值范围是（　　）
分析：圆x2+y2-2y=0的圆心是（0，1），半径r=1，抛物线y2=4ax的准线x=a，由抛物线y2=4ax的准线与圆x2+y2-2y=0相离，能求出实数a的取值范围．
解答：解：圆x2+y2-2y=0的圆心是（0，1），半径r=1，
抛物线y2=4ax的准线x=a，
∵抛物线y2=4ax的准线与圆x2+y2-2y=0相离，
∴a＜-1或a＞1．
故选D．
点评：本题考查圆的性质和应用，解题时要注意抛物线的准线方程的灵活运用．
练习册系列答案
相关题目
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
（2003•东城区二模）已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（Ⅰ）求点P和Q的坐标；
（Ⅱ）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程；
（Ⅲ）设点A（t，0）（常数t＞4），当a在闭区间〔1，2〕内变化时，求△APQ面积的最大值，并求相应a的值．
已知抛物线y2=4a（x+a）（a＞0），过原点O作一直线交抛物线于A、B两点，如图所示，试求|OA|·|OB|的最小值。
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
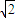已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为，过抛物线C1的焦点F作倾斜角为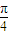的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网