题目内容
2.已知F1(-1,0)和F2(1,0)是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个焦点,且点$P(1\;,\;\frac{3}{2})$在椭圆C上.(Ⅰ)求椭圆C的方程;
(Ⅱ)直线l:y=kx+m(m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线l的方程.
分析 (Ⅰ)由F1(-1,0)和F2(1,0)是椭圆的两个焦点,且点$P(1\;,\;\frac{3}{2})$在椭圆C上,求出a,b,由此能求出椭圆C的方程.
(Ⅱ)由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+m\end{array}\right.$,得(4k2+3)x2+8kmx+4m2-12=0,由此利用根的判别式、韦达定理、弦长公式、基本不等式、椭圆性质,结合已知条件能求出直线方程.
解答 (共13分)
解:(Ⅰ)∵F1(-1,0)和F2(1,0)是椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个焦点,且点$P(1\;,\;\frac{3}{2})$在椭圆C上,
∴依题意,c=1,又$2a=\sqrt{{{(1+1)}^2}+{{(\frac{3}{2}-0)}^2}}+\frac{3}{2}=\frac{8}{2}=4$,故a=2.
所以b2=3.
故所求椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(Ⅱ)由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+m\end{array}\right.$,消y得(4k2+3)x2+8kmx+4m2-12=0,
由直线l与椭圆C仅有一个公共点知,
△=64k2m2-4(4k2+3)(4m2-12)=0,整理得m2=4k2+3. …(6分)
由条件可得k≠0,$M(-\frac{m}{k}\;,\;0)$,N(0,m).
所以${S_{△OMN}}=\frac{1}{2}|{OM}|•|{ON}|=\frac{1}{2}|m|•|{\frac{m}{k}}|=\frac{m^2}{2|k|}$. ①
将m2=4k2+3代入①,得${S_{△OMN}}=\frac{1}{2}•\frac{{4{k^2}+3}}{|k|}=\frac{1}{2}(4|k|+\frac{3}{|k|})$.
因为|k|>0,所以${S_{△OMN}}=\frac{1}{2}(4|k|+\frac{3}{|k|})≥2\sqrt{3}$,
当且仅当$|k|=\frac{{\sqrt{3}}}{2}$,即$k=±\frac{{\sqrt{3}}}{2}$时等号成立,S△OMN有最小值$2\sqrt{3}$.
因为m2=4k2+3,所以m2=6,又m>0,解得$m=\sqrt{6}$.…(11分)
故所求直线方程为$y=\frac{{\sqrt{3}}}{2}x+\sqrt{6}$或$y=-\frac{{\sqrt{3}}}{2}x+\sqrt{6}$. …(13分)
点评 本题考查椭圆方程的求法,考查直线方程的求法,是中档硅化木,解题时要认真审题,注意根的判别式、韦达定理、弦长公式、基本不等式、椭圆性质的合理运用.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案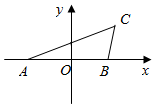 如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.
如图,A(-2,0),B(2,0),第一象限内点C满足∠ACB=60°,且△ABC的面积为$\sqrt{3}$.双曲线Г以A、B为焦点,经过点C.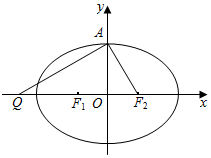 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且F1恰是QF2的中点.若过A、Q、F2三点的圆恰好与直线l:x-$\sqrt{3}$y-3=0相切.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且F1恰是QF2的中点.若过A、Q、F2三点的圆恰好与直线l:x-$\sqrt{3}$y-3=0相切. 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点到直线x-y+3$\sqrt{2}$=0的距离为5,且椭圆的一个长轴端点与一个短轴端点间的距离为$\sqrt{10}$.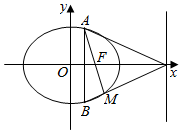 如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).
如图,已知椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,F为该椭圆的右焦点,若AB为垂直于x轴的动弦,直线l:x=4与x轴交于点N,直线AF与BN交于点M(x0,y0).