题目内容
已知数列{
}的前n项和
，数列{
}满足=
．
（I）求证数列{}是等差数列，并求数列{}的通项公式；
（Ⅱ）设
，数列{
}的前n项和为Tn，求满足
的n的最大值。
解：（Ⅰ）在
中，令n=1，可得
，即
．
当
时，
∴
， …
∴
，即
．∵
，∴
，即当时，
．又
，∴数列{bn}是首项和公差均为1的等差数列．
于是
，∴
． …………………………6分
（Ⅱ）∵
,∴
,………………8分
∴
=
．10分
由
，得，即
，
单调递减，∵
，∴
的最大值为4．
练习册系列答案
相关题目
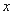，已知甲、乙两组的平均成绩相同.
过点
，则
的最小值为_______________．
确定的平面区域记为
，不等式
确定的平面区域记为
，在
B．
C．
D．
的部分图像如图，令
则
．
，则这个圆锥的全面积是( )
是等差数列，
，且
，
，
成等比数列．
，求数列
的前
项和
．
的单调递增区间；
,求