题目内容
已知正项等比数列{ }中,
}中, ,
, 成等差数列,则
成等差数列,则 ( )
( )
A. | B. | C. | D. |
D
解析试题分析:因为 ,
, 成等差数列,所以
成等差数列,所以 ,根据等比数列通项公式展开可得
,根据等比数列通项公式展开可得 ,因为数列是正项等比数列,所以
,因为数列是正项等比数列,所以 ,消取
,消取 ,解得
,解得 ,将所求展开代入,可得
,将所求展开代入,可得 .
.
考点:等差中项,等比通项公式.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知数列 为等差数列,且
为等差数列,且 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
已知等差数列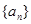 单调递增且满足
单调递增且满足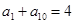 ,则
,则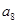 的取值范围是( )
的取值范围是( )
A.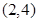 | B.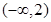 | C.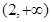 | D.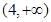 |
已知等差数列{an}中,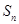 是它的前n项和.若S16>0,且
是它的前n项和.若S16>0,且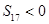 ,则当
,则当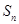 最大时n的值为( )
最大时n的值为( )
| A.8 | B.9 | C.10 | D.16 |
若1,a,4成等比数列,3,b,5成等差数列,则 的值是( )
的值是( )
A. | B. | C.±2 | D. |
数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
| A.3690 | B.3660 | C.1845 | D.1830 |
已知等差数列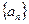 的首项为
的首项为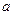 ,公差为
,公差为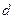 ,且方程
,且方程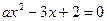 的解为
的解为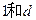 ,则数列{
,则数列{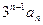 }的前n项和
}的前n项和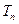 为( )
为( )
A.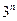 |
B.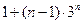 |
C.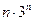 |
D.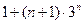 |
 尺
尺 尺
尺 尺
尺 尺
尺
