题目内容
椭圆M: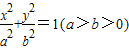 的左、右焦点分别为F1,F2,P为椭圆M上任一点,且PF1•PF2的最大值为3c2,其中c2=a2-b2,则椭圆M的离心率为 .
的左、右焦点分别为F1,F2,P为椭圆M上任一点,且PF1•PF2的最大值为3c2,其中c2=a2-b2,则椭圆M的离心率为 .
【答案】分析:先根据题意得到两焦点的坐标,设出点P的坐标进而可表示出 、
、 ,再得到二者的数量积后将
,再得到二者的数量积后将 代入消去x得到关于y的关系式,进而可得到当y=0时
代入消去x得到关于y的关系式,进而可得到当y=0时 •
• 的值取到最大,进而可求出离心率.
的值取到最大,进而可求出离心率.
解答:解:由题意可知F1(-c,0),F2(c,0),设点P为(x,y)
∵ ∴
∴
∴ ,
,
∴ =x2-c2+y2=
=x2-c2+y2= -c2+y2
-c2+y2
=
当y=0时 取到最大值3c2,即a2-c2=3c2,
取到最大值3c2,即a2-c2=3c2,
∴a2=4c2∴e= =
=
故答案为:
点评:本题主要考查向量的数量积运算和椭圆的简单性质.考查对基础知识的综合运用.
 、
、 ,再得到二者的数量积后将
,再得到二者的数量积后将 代入消去x得到关于y的关系式,进而可得到当y=0时
代入消去x得到关于y的关系式,进而可得到当y=0时 •
• 的值取到最大,进而可求出离心率.
的值取到最大,进而可求出离心率.解答:解:由题意可知F1(-c,0),F2(c,0),设点P为(x,y)
∵
 ∴
∴
∴
 ,
,
∴
 =x2-c2+y2=
=x2-c2+y2= -c2+y2
-c2+y2=

当y=0时
 取到最大值3c2,即a2-c2=3c2,
取到最大值3c2,即a2-c2=3c2,∴a2=4c2∴e=
 =
=
故答案为:

点评:本题主要考查向量的数量积运算和椭圆的简单性质.考查对基础知识的综合运用.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.
 的左、右焦点分别为F1,F2,P为椭圆M上任一点,且PF1•PF2的最大值为3c2,其中c2=a2-b2,则椭圆M的离心率为 ________.
的左、右焦点分别为F1,F2,P为椭圆M上任一点,且PF1•PF2的最大值为3c2,其中c2=a2-b2,则椭圆M的离心率为 ________.