题目内容
设函数 ,则满足f(x)≥0的x的取值范围是 ________.
,则满足f(x)≥0的x的取值范围是 ________.
[2,3]
分析:将“f(x)≥0”,用对数函数的单调性转化为“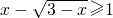 ”,再令
”,再令 ,转化为一元二次不等式求解.
,转化为一元二次不等式求解.
解答:∵f(x)≥0,函数 ,
,
∴可转化为: ≥0
≥0
由对数函数的单调性可转化为:
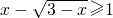
令 ,
,
不等式可转化为:
t2+t-2≤0
解得:0≤t≤1
∴2≤x≤3
故答案为:[2,3]
点评:本题主要考查用函数单调性和换元法求解不等式,这种方式不仅反映了不等式,同时也考查了函数的图象和性质,这是目前不等式考查的主流,应引起足够的重视.
分析:将“f(x)≥0”,用对数函数的单调性转化为“
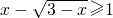 ”,再令
”,再令 ,转化为一元二次不等式求解.
,转化为一元二次不等式求解.解答:∵f(x)≥0,函数
 ,
,∴可转化为:
 ≥0
≥0由对数函数的单调性可转化为:
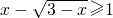
令
 ,
,不等式可转化为:
t2+t-2≤0
解得:0≤t≤1
∴2≤x≤3
故答案为:[2,3]
点评:本题主要考查用函数单调性和换元法求解不等式,这种方式不仅反映了不等式,同时也考查了函数的图象和性质,这是目前不等式考查的主流,应引起足够的重视.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则满足f(x)=
,则满足f(x)= 的x值为( )
的x值为( )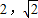

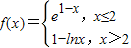 ,则满足f(x)≤1的x的取值范围是( )
,则满足f(x)≤1的x的取值范围是( )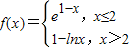 ,则满足f(x)≤1的x的取值范围是( )
,则满足f(x)≤1的x的取值范围是( )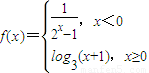 ,则满足|f(x)|<2的x的取值范围是( )
,则满足|f(x)|<2的x的取值范围是( ) ,则满足f(x)≤2的x的取值范围是 .
,则满足f(x)≤2的x的取值范围是 .