题目内容
设函数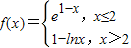 ,则满足f(x)≤1的x的取值范围是( )
,则满足f(x)≤1的x的取值范围是( )A.[1,2]
B.[0,2]
C.[1,+∞)
D.[0,+∞)
【答案】分析:由不等式f(x)≤1可得① ,或②
,或② .分别求出①、②的解集,再取并集,即得所求.
.分别求出①、②的解集,再取并集,即得所求.
解答:解:∵函数 ,则由不等式f(x)≤1可得①
,则由不等式f(x)≤1可得① ,或②
,或② .
.
解①可得,1≤x≤2 解②可得 x>2.
综上可得 x的取值范围是[1,+∞),
故选C.
点评:本题主要考查指数不等式对数不等式的解法,指数函数和对数函数的单调性及特殊点,体现了分类讨论的数学思想,属于中档题.
 ,或②
,或② .分别求出①、②的解集,再取并集,即得所求.
.分别求出①、②的解集,再取并集,即得所求.解答:解:∵函数
 ,则由不等式f(x)≤1可得①
,则由不等式f(x)≤1可得① ,或②
,或② .
.解①可得,1≤x≤2 解②可得 x>2.
综上可得 x的取值范围是[1,+∞),
故选C.
点评:本题主要考查指数不等式对数不等式的解法,指数函数和对数函数的单调性及特殊点,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ,则满足f(x)=
,则满足f(x)= 的x值为( )
的x值为( )

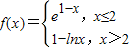 ,则满足f(x)≤1的x的取值范围是( )
,则满足f(x)≤1的x的取值范围是( )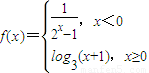 ,则满足|f(x)|<2的x的取值范围是( )
,则满足|f(x)|<2的x的取值范围是( ) ,则满足f(x)≤2的x的取值范围是 .
,则满足f(x)≤2的x的取值范围是 .