题目内容
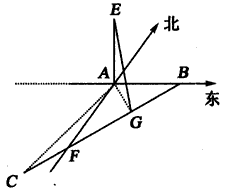
某人在塔的正东沿着南偏西60°的方向前进40m后,望见塔在东北,若沿途测得塔的最大仰角为30°,求塔高。
| 解:设B为塔正东方向一点,AE为塔, 沿南偏西60°行走40m后到达C处, 即BC=40,且∠CAB=135°,∠ABC=30°, 如图,在△ABC中, 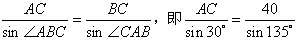 , ,∴AC= 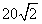 , ,由点A向BC作垂线AG,此时仰角∠AGE最大,等于30°, 在△ABC中, 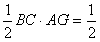 AC·BC·sin∠ACB, AC·BC·sin∠ACB,∴ 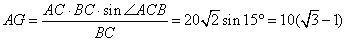 , ,∴在△AEG中, 塔高AE=AG·tan30°= 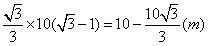 , , ∴塔高为 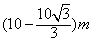 。 。 |
 |

练习册系列答案
相关题目