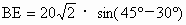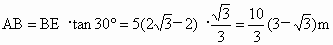题目内容
某人在塔的正东沿着南
60°西的方向前进40m以后望见塔在东北,若沿途测得塔的最大仰角为30°,求塔高.
答案:略
解析:
提示:
解析:
|
解:在△ DBC中,由正弦定理可得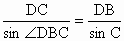 , ,
∴ 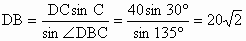 . .
∵∠ AEB为最大仰角,∴ 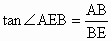 ,AB为定值. ,AB为定值.
要使∠ AEB最大,BE应最小,则所求 BE应是点B到DC的最短距离.∴ 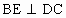 . .
在 Rt△DBE中,BE=DBsin15°,
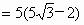 . .
在 Rt△AEB中,
|
提示:
|
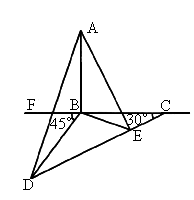
依题意作图,则∠C=30°,∠FBD=45°,CD=40,由此得∠DBC=180°-45°=135°,∠BDC=15° |

练习册系列答案
相关题目