题目内容
已知△AOB,点P在直线AB上,且满足 =2t
=2t +t
+t (t∈R),则t=________.
(t∈R),则t=________.
1
分析:首先用 表示
表示 :
: ,将这个式子代入已知等式可得用
,将这个式子代入已知等式可得用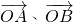 表示
表示 的式子.再根据点P在直线AB上设出
的式子.再根据点P在直线AB上设出 ,得到用
,得到用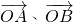 表示
表示 的另一个表达式,最后结合平面向量基本定理,得到两个表达式的对应系数相等,从而得出t的值.
的另一个表达式,最后结合平面向量基本定理,得到两个表达式的对应系数相等,从而得出t的值.
解答:∵ ,
, =2t
=2t +t
+t
∴ =2t(
=2t(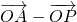 )+t
)+t
∴ =
= +
+
∵点P在直线AB上,
∴ ?
?
根据平面向量基本定理,得 ?
?
解之得t=1
故答案为:1
点评:本题考查了平面向量基本定理的应用,是一道中档题.平面向量基本定理:用平面内两个不共线的向量可以线性表示平面内任意第三个向量,并且这种表示是唯一的.
分析:首先用
 表示
表示 :
: ,将这个式子代入已知等式可得用
,将这个式子代入已知等式可得用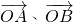 表示
表示 的式子.再根据点P在直线AB上设出
的式子.再根据点P在直线AB上设出 ,得到用
,得到用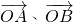 表示
表示 的另一个表达式,最后结合平面向量基本定理,得到两个表达式的对应系数相等,从而得出t的值.
的另一个表达式,最后结合平面向量基本定理,得到两个表达式的对应系数相等,从而得出t的值.解答:∵
 ,
, =2t
=2t +t
+t
∴
 =2t(
=2t(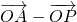 )+t
)+t
∴
 =
= +
+
∵点P在直线AB上,
∴
 ?
?
根据平面向量基本定理,得
 ?
?
解之得t=1
故答案为:1
点评:本题考查了平面向量基本定理的应用,是一道中档题.平面向量基本定理:用平面内两个不共线的向量可以线性表示平面内任意第三个向量,并且这种表示是唯一的.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知△AOB,点P在直线AB上,且满足
=2t
+t
(t∈R),则t=( )
. |
| OP |
. |
| PA |
. |
| OB |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|