题目内容
已知三点A（a，0）、B（0，b），C（4，1）共线，其中a•b＞0，则a+b的最小值为（ ）
| A、8 | ||
B、7
| ||
| C、9 | ||
D、10
|
分析：三点共线即两个向量共线，据两向量共线的充要条件求出a，b的关系，据已知条件a•b＞0知b-1＞0，
将a，b关系代入a+b消去a，凑成乘积为定值，利用基本不等式求出最小值．
将a，b关系代入a+b消去a，凑成乘积为定值，利用基本不等式求出最小值．
解答：解：
=(-a，b)，
=(4-a，1)
∵A（a，0）、B（0，b），C（4，1）共线
∴
，
共线
∴-a=4b-ab
∴a=
∵a•b＞0
∴b-1＞0
∴a+b=
+b=
+b-1+5≥9
当且仅当b=3时取等号
故a+b的最小值为9
故选项为C
| AB |
| AC |
∵A（a，0）、B（0，b），C（4，1）共线
∴
| AB |
| AC |
∴-a=4b-ab
∴a=
| 4b |
| b-1 |
∵a•b＞0
∴b-1＞0
∴a+b=
| 4b |
| b-1 |
| 4 |
| b-1 |
当且仅当b=3时取等号
故a+b的最小值为9
故选项为C
点评：本题考查两向量共线的充要条件及利用基本不等式求函数的最值需注意：一正、二定，三相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
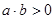，则a+b的最小值为（ ）
C．9 D．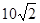 
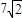
），以A、B为焦点的椭圆经过点C。
轴的直线
与椭圆交于不同两点M、N，使
？若存在，求出直线l斜率的取值范围；若不存在，请说明理由；
轴上的点P（0，n）（
），存在不平行于
，试求n的取值范围。
）；以A、B为焦点的椭圆经过C点，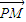
+
）•
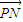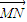=0？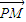
+
）•
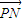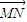=0，试求实数n的取值范围．