题目内容
已知向量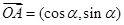 (
(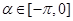 ),向量
),向量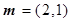 ,
,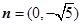 ,
,
且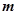
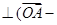
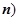 .
.
(Ⅰ)求向量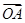 ; (Ⅱ)若
; (Ⅱ)若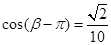 ,
,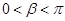 ,求
,求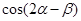 .
.
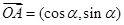 (
(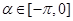 ),向量
),向量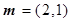 ,
,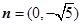 ,
,且
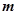
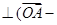
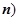 .
.(Ⅰ)求向量
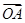 ; (Ⅱ)若
; (Ⅱ)若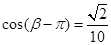 ,
,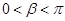 ,求
,求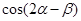 .
.(Ⅰ)∴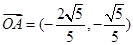 ……………6分
……………6分
(Ⅱ)∴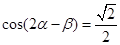 .
.
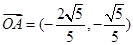 ……………6分
……………6分(Ⅱ)∴
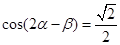 .
.本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵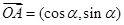 ,∴
,∴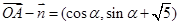 ,…………………1分
,…………………1分
∵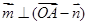 ,得到三角关系是
,得到三角关系是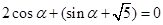 ,结合
,结合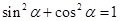 ,解得。
,解得。
(2)由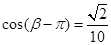 ,解得
,解得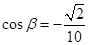 ,
,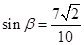 ,结合二倍角公式
,结合二倍角公式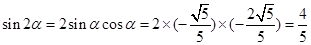 ,和
,和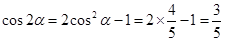 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵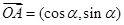 ,∴
,∴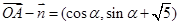 ,…………1分
,…………1分
∵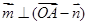 ,∴
,∴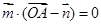 ,即
,即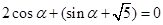 ① …………2分
① …………2分
又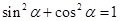 ② 由①②联立方程解得,
② 由①②联立方程解得,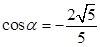 ,
,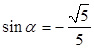 5分
5分
∴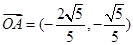 ……………6分
……………6分
(Ⅱ)∵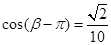 即
即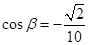 ,
,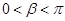 , …………7分
, …………7分
∴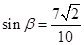 ,
,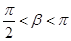 ………8分
………8分
又∵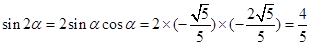 , ………9分
, ………9分
 , ……10分
, ……10分
∴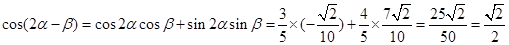 .
.
解法二: (Ⅰ)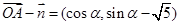 ,…………………………………1分
,…………………………………1分
又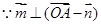 ,∴
,∴ ,即
,即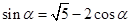 ,①……2分
,①……2分
又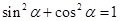 ②
②
将①代入②中,可得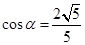 ③ …………………4分
③ …………………4分
将③代入①中,得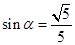 ……………………………………5分
……………………………………5分
∴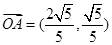 …………………………………6分
…………………………………6分
(Ⅱ) 方法一 ∵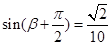 ,
,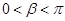 ,∴
,∴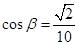 ,且
,且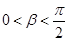 ……7分
……7分
∴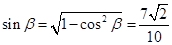 ,从而
,从而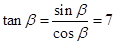 . …………………8分
. …………………8分
由(Ⅰ)知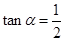 ,
, 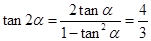 ; ………………9分
; ………………9分
∴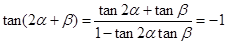 . ………………………………10分
. ………………………………10分
又∵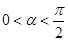 ,∴
,∴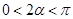 , 又
, 又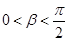 ,∴
,∴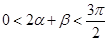 ……11分
……11分
综上可得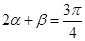 ………………………………12分
………………………………12分
方法二∵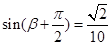 ,
,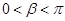 ,∴
,∴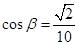 ,且
,且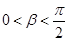 …………7分
…………7分
∴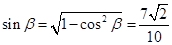 . ……………8分
. ……………8分
由(Ⅰ)知 ,
,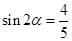 . …………9分
. …………9分
∴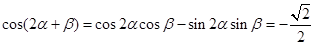 ……………10分
……………10分
∵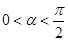 ,且注意到
,且注意到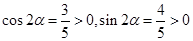 ,
,
∴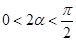 ,又
,又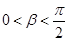 ,∴
,∴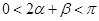 ………………………11分
………………………11分
综上可得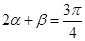 …………………12分
…………………12分
(若用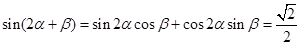 ,又∵
,又∵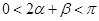 ∴
∴ 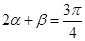 ,
,
(1)问中∵
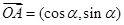 ,∴
,∴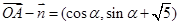 ,…………………1分
,…………………1分∵
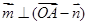 ,得到三角关系是
,得到三角关系是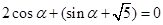 ,结合
,结合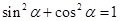 ,解得。
,解得。(2)由
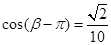 ,解得
,解得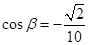 ,
,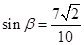 ,结合二倍角公式
,结合二倍角公式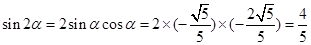 ,和
,和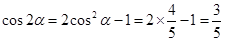 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。解析一:(Ⅰ)∵
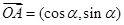 ,∴
,∴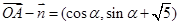 ,…………1分
,…………1分∵
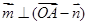 ,∴
,∴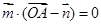 ,即
,即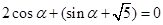 ① …………2分
① …………2分又
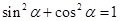 ② 由①②联立方程解得,
② 由①②联立方程解得,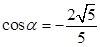 ,
,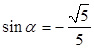 5分
5分∴
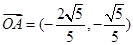 ……………6分
……………6分(Ⅱ)∵
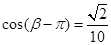 即
即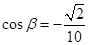 ,
,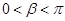 , …………7分
, …………7分∴
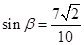 ,
,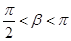 ………8分
………8分又∵
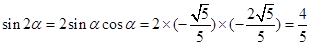 , ………9分
, ………9分 , ……10分
, ……10分∴
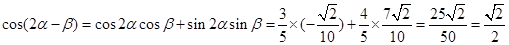 .
.解法二: (Ⅰ)
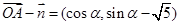 ,…………………………………1分
,…………………………………1分又
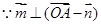 ,∴
,∴ ,即
,即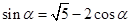 ,①……2分
,①……2分又
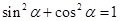 ②
②将①代入②中,可得
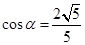 ③ …………………4分
③ …………………4分将③代入①中,得
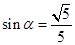 ……………………………………5分
……………………………………5分∴
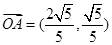 …………………………………6分
…………………………………6分(Ⅱ) 方法一 ∵
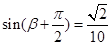 ,
,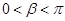 ,∴
,∴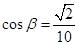 ,且
,且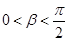 ……7分
……7分∴
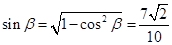 ,从而
,从而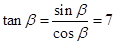 . …………………8分
. …………………8分由(Ⅰ)知
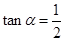 ,
, 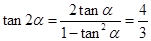 ; ………………9分
; ………………9分∴
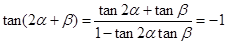 . ………………………………10分
. ………………………………10分又∵
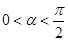 ,∴
,∴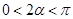 , 又
, 又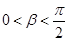 ,∴
,∴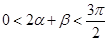 ……11分
……11分综上可得
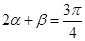 ………………………………12分
………………………………12分方法二∵
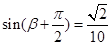 ,
,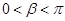 ,∴
,∴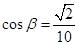 ,且
,且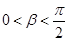 …………7分
…………7分∴
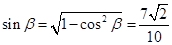 . ……………8分
. ……………8分由(Ⅰ)知
 ,
,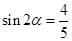 . …………9分
. …………9分∴
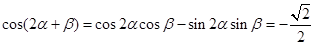 ……………10分
……………10分∵
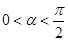 ,且注意到
,且注意到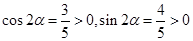 ,
,∴
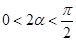 ,又
,又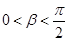 ,∴
,∴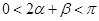 ………………………11分
………………………11分综上可得
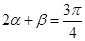 …………………12分
…………………12分(若用
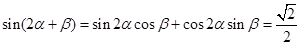 ,又∵
,又∵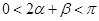 ∴
∴ 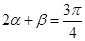 ,
,
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 ,
, 满足
满足 ,
, ,则
,则 ,②
,② , ③
, ③  ,④
,④ 中一定可以充当平面向量一组基底的是( )
中一定可以充当平面向量一组基底的是( ) .
. ,求
,求 的夹角。
的夹角。  为45°,求
为45°,求 的值;
的值; .
. ;
; ,求
,求 的最小值、最大值.
的最小值、最大值.
 ,
, ).
). |=|
|=| |,求角α的值;
|,求角α的值; 的值.
的值.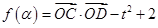 在定义域α∈(
在定义域α∈( ,求
,求 的值。
的值。 中,点
中,点 在
在 上,
上, 平分
平分 .若
.若 ,
, ,
, ,
, ,则
,则 ( )
( )



 为
为 的边
的边 上一点,
上一点, 为
为
 ,则
,则 ( )
( )
