题目内容
 是定义在
是定义在 上的函数,
上的函数, 则“
则“ 均为偶函数”是“
均为偶函数”是“ 为偶函数”的( )
为偶函数”的( )
| A.充要条件 | B.充分而不必要条件 |
| C.必要而不充分条件 | D.既不充分也不必要条件 |
B
解析试题分析:由于 是定义在
是定义在 上的函数,说明函数
上的函数,说明函数 定义域关于原点对称,同时当条件成立时,即
定义域关于原点对称,同时当条件成立时,即 均为偶函数”,则可知f(-x)="f(x)," g(-x)=g(x),那么根据偶函数定义可知h(-x)=" f(-x)+g(-x)=" f(x)+g(x)=h(x),因此可知为偶函数.反之则当h(x)=
均为偶函数”,则可知f(-x)="f(x)," g(-x)=g(x),那么根据偶函数定义可知h(-x)=" f(-x)+g(-x)=" f(x)+g(x)=h(x),因此可知为偶函数.反之则当h(x)= =
= 显然是偶函数,但是f(x)
显然是偶函数,但是f(x) 不是偶函数,结论不能推出条件,故选B。
不是偶函数,结论不能推出条件,故选B。
考点:本题主要是考查函数奇偶性的运用。
点评:解决该试题的关键是能根据函数的偶函数的定义得到由条件可以判定结论成立,同时当结论成立的时候可以举出反例说明不一定成立。

练习册系列答案
相关题目
“1<a<2”是“对任意的正数x,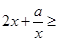 2”的
2”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
命题“若一个数是负数,则它的平方是正数”的逆命题是 ( )
| A.“若一个数是负数,则它的平方不是正数” |
| B.“若一个数的平方是正数,则它是负数” |
| C.“若一个数不是负数,则它的平方不是正数” |
| D.“若一个数的平方不是正数,则它不是负数” |
命题“若 则
则 ”的逆否命题是( )
”的逆否命题是( )
A.若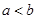 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
已知命题 ,则 ( )
,则 ( )
A. | B. |
C.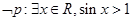 | D.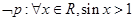 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设p、q是两上命题, ( )
( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“m=4”是“直线(m+2)x+2my-1=0与直线(m+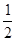 )x+(m+2)y+3=0相互平行”的
)x+(m+2)y+3=0相互平行”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要 |
命题“对任意的 ”的否定是( )
”的否定是( )
A.不存在 | B.存在 |
C.存在 | D.对任意的 |