题目内容
当x>0时,证明不等式ex>1+x+
证明:设f(x)=ex-1-x![]() x2,f′(x)=ex-1-x,下面证明g(x)=ex-1-x在x>0时恒为正.
x2,f′(x)=ex-1-x,下面证明g(x)=ex-1-x在x>0时恒为正.
∵g′(x)=ex-1,若x>0时,g′(x)>0,∴g(x)在(0,+∞)上是增函数,当x>0时,g(x)>g(0)=0,
即f′(x)在(0,+∞)上恒为正,∴f(x)在(0,+∞)上是增函数,又f(0)=e0-1-0-0=0,∴x>0时,f(x)>f(0)=0,
即ex>1+x+![]() x2成立.
x2成立.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 的定义域为[a,b].
的定义域为[a,b]. ,若对任意的
,若对任意的 ,总存在
,总存在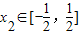 ,使得f(x2)=g(x1)成立,求实数m的取值范围.
,使得f(x2)=g(x1)成立,求实数m的取值范围. 的定义域为[a,b].
的定义域为[a,b]. ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得f(x2)=g(x1)成立,求实数m的取值范围.
,使得f(x2)=g(x1)成立,求实数m的取值范围.