题目内容
(14分)已知函数 ,
, ,记
,记 .
.
(1)若 ,且
,且 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(2)若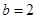 ,且
,且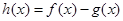 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(3)若 ,设函数
,设函数 的图象
的图象 与函数
与函数 图象
图象 交于点
交于点 、
、 ,过线段
,过线段 的中点作
的中点作 轴的垂线分别交
轴的垂线分别交 ,
, 于点
于点 、
、 ,请判断
,请判断 在点
在点 处的切线与
处的切线与 在点
在点 处的
处的 切线能否平行,并说明你的理由.
切线能否平行,并说明你的理由.
 ,
, ,记
,记 .
.(1)若
 ,且
,且 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;(2)若
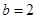 ,且
,且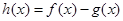 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;(3)若
 ,设函数
,设函数 的图象
的图象 与函数
与函数 图象
图象 交于点
交于点 、
、 ,过线段
,过线段 的中点作
的中点作 轴的垂线分别交
轴的垂线分别交 ,
, 于点
于点 、
、 ,请判断
,请判断 在点
在点 处的切线与
处的切线与 在点
在点 处的
处的 切线能否平行,并说明你的理由.
切线能否平行,并说明你的理由.(1)不等式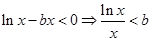 ,函数
,函数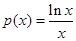
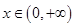 ,
,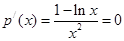 ,
,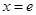 ,
,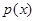 先增后减
先增后减
最大值为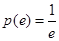 ,
, 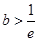
(2)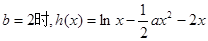 ,
,
则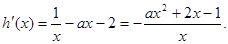
当 时,
时,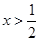 时,
时,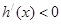 ,函数为减函数;
,函数为减函数;
当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,
-1<a<0,
综上: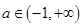
(3)不能平行。
设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为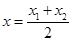
假设C1在点M处的切线与C2在点N处的切线平行得:
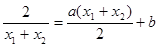 ,点P、Q的坐标代入函数表达式
,点P、Q的坐标代入函数表达式
两式相减得: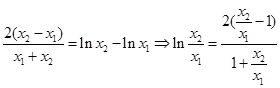
设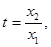 则
则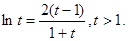 令
令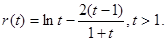
得用导数得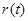 在
在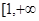 )上单调递增. 故
)上单调递增. 故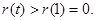
所以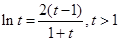 不成立,即两切线不可能平行。
不成立,即两切线不可能平行。
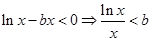 ,函数
,函数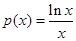
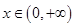 ,
,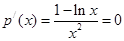 ,
,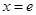 ,
,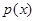 先增后减
先增后减最大值为
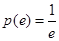 ,
, 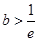
(2)
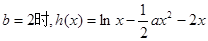 ,
,则
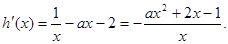
当
 时,
时,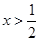 时,
时,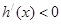 ,函数为减函数;
,函数为减函数;当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,
-1<a<0,
综上:
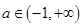
(3)不能平行。
设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为
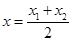
假设C1在点M处的切线与C2在点N处的切线平行得:
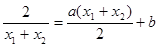 ,点P、Q的坐标代入函数表达式
,点P、Q的坐标代入函数表达式两式相减得:
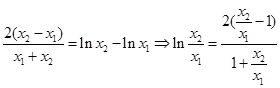
设
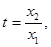 则
则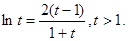 令
令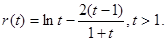
得用导数得
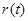 在
在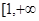 )上单调递增. 故
)上单调递增. 故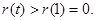
所以
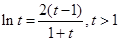 不成立,即两切线不可能平行。
不成立,即两切线不可能平行。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,正实数a,b,c满足
,正实数a,b,c满足 且
且 。
。 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:① ;②
;② ③
③ ④
④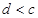 中有可能成立的个数为( )
中有可能成立的个数为( ) 上的函数
上的函数 满足下列两个条件:⑴对任意的
满足下列两个条件:⑴对任意的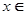
 成立;⑵当
成立;⑵当 时,
时, ;如果关于
;如果关于 的方程
的方程 恰有两个不同的解,那么实数
恰有两个不同的解,那么实数 的取值范围是 .
的取值范围是 .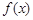 的定义域为
的定义域为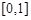 ,且同时满足:①
,且同时满足:①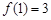 ;②
;②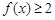 恒成立;③若
恒成立;③若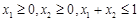 ,则有
,则有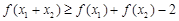 .
.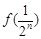 与
与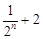 的大小
的大小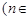 N);
N);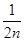 (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1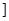 ,都有
,都有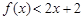 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由. 增加4万元,从第一年起每年蔬菜销售收入50万元.设
增加4万元,从第一年起每年蔬菜销售收入50万元.设 表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元).
表示前n年的纯利润总和,(f(n)=前n年的总收入–前n年的总支出–投资额72万元). (I)该厂从第几年开始盈利?
(I)该厂从第几年开始盈利? ,其中
,其中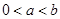 .
.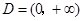 时,设
时,设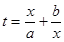 ,
,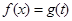 ,求
,求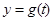 的解析式及定义域;
的解析式及定义域;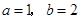 时,求
时,求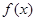 的最小值;
的最小值;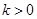 ,当
,当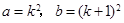 时,
时,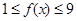 对任意
对任意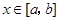 恒成立,求
恒成立,求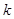 的取值范围.
的取值范围.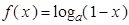 ,
,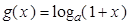 (
(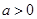 且
且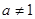 )。
)。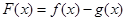 ,判断
,判断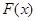 的奇偶性并证明;
的奇偶性并证明;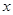 的方程
的方程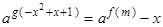 有两个不等实根,求实数
有两个不等实根,求实数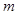 的范围;
的范围;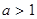 且在
且在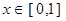 时,
时,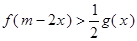 恒成立,求实数
恒成立,求实数 ,那么
,那么 =________.
=________. 必过定点__ ▲ ___
必过定点__ ▲ ___