题目内容
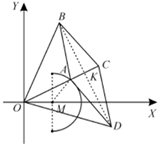 如图,在平面直角坐标系XOY中,菱形ABCD的边长为4,且|OB|=|OD|=6.
如图,在平面直角坐标系XOY中,菱形ABCD的边长为4,且|OB|=|OD|=6.(Ⅰ)求证:|OA|.|OC|为定值;
(Ⅱ)当点A在半圆(x-2)2+y2=4(2≤x≤4)上运动时,求点C的轨迹.
分析:(Ⅰ)根据题目给出的条件四边形ABCD为菱形,且|OB|=|OD|,得到O、A、C三点共线,连结BD,则BD垂直平分线段AC,设垂足为K,然后把|OA|•|OC|通过|0K|和|AK|转化为用|OB|和|AB|表示,则答案可证;
(Ⅱ)设出C点坐标,把A的坐标用∠XMA表示,得到|OA|,结合(Ⅰ)中结论求出C的横坐标为定值5,进一步求出C的纵坐标的范围,则点C的轨迹可求.
(Ⅱ)设出C点坐标,把A的坐标用∠XMA表示,得到|OA|,结合(Ⅰ)中结论求出C的横坐标为定值5,进一步求出C的纵坐标的范围,则点C的轨迹可求.
解答: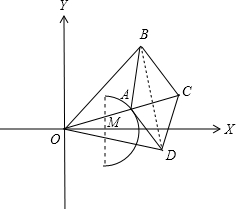 解:(Ⅰ)如图,
解:(Ⅰ)如图,
∵|OB|=|OD|,|AB|=|AD|=|BC|=|CD|,∴O、A、C三点共线,
连结BD,则BD垂直平分线段AC,设垂足为K,于是有
|OA|•|OC|=(|OK|-|AK|)(|OK|+|AK|)
=|OK|2-|AK|2=(|OB|2-|BK|2)(|AB|2-|BK|2)
=|OB|2-|AB|2=62-42=20(定值);
(Ⅱ)设C(x,y),A(2+2cosα,sinα),其中α=∠XMA(-
≤α≤
),
则∠XOC=
.
∵|OA|2=(2+2cosα)2+(2sinα)2=8(1+cosα)=16cos2
,
∴|OA|=4cos
.
由(Ⅰ)的结论得:|OC|cos
=5,∴x=|OC|cos
=5.
从而y=|OC|sin
=5tan
∈[-5,5].
故点C的轨迹是一条线段,其两个短点的坐标分别为A(5,5),B(5,-5).
 解:(Ⅰ)如图,
解:(Ⅰ)如图,∵|OB|=|OD|,|AB|=|AD|=|BC|=|CD|,∴O、A、C三点共线,
连结BD,则BD垂直平分线段AC,设垂足为K,于是有
|OA|•|OC|=(|OK|-|AK|)(|OK|+|AK|)
=|OK|2-|AK|2=(|OB|2-|BK|2)(|AB|2-|BK|2)
=|OB|2-|AB|2=62-42=20(定值);
(Ⅱ)设C(x,y),A(2+2cosα,sinα),其中α=∠XMA(-
| π |
| 2 |
| π |
| 2 |
则∠XOC=
| α |
| 2 |
∵|OA|2=(2+2cosα)2+(2sinα)2=8(1+cosα)=16cos2
| α |
| 2 |
∴|OA|=4cos
| α |
| 2 |
由(Ⅰ)的结论得:|OC|cos
| α |
| 2 |
| α |
| 2 |
从而y=|OC|sin
| α |
| 2 |
| α |
| 2 |
故点C的轨迹是一条线段,其两个短点的坐标分别为A(5,5),B(5,-5).
点评:本题考查了轨迹方程,考查了数形结合的解题思想方法和数学转化思想方法,解答的关键是利用平面几何知识把未知长度的式子转化为已知长度的式子,是中档题.

练习册系列答案
相关题目
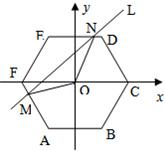 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
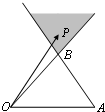 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是