题目内容
数列{an}满足:a1=1,an+1= an+1.
an+1.(1)写出a2,a3,a4.
(2)求数列{an}的通项公式.
【答案】分析:(1)通过a1=1,an+1= an+1.利用n=2,3,4,即可求出a2,a3,a4.
an+1.利用n=2,3,4,即可求出a2,a3,a4.
(2)解法一:通过(1)猜想数列的通项公式,然后利用数学归纳法证明;
解法二:构造{bn}是以b1=-1, 为公比的等比数列,求出bn然后求数列{an}的通项公式.
为公比的等比数列,求出bn然后求数列{an}的通项公式.
解答:解:(1)因为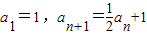 ,
,
所以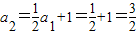 ,
,
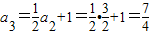 ,
,
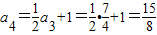 .-------------------(3分)
.-------------------(3分)
(2)解法一:猜想: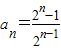 .下面用数学归纳法证明,
.下面用数学归纳法证明,
证明:(1)当n=1时,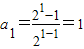 ,满足上式,显然成立;-------------------(4分)
,满足上式,显然成立;-------------------(4分)
(2)假设当n=k时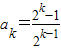 ,那么当n=k+1时,
,那么当n=k+1时,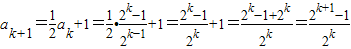 满足上式,
满足上式,
即当n=k+1时猜想也成立.-------------------(7分)
由(1)(2)可知,对于n∈n*都有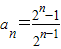 .------------------(8分)
.------------------(8分)
解法二:因为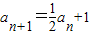 ,所以
,所以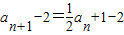 ,即
,即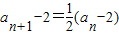 ,-------(4分)
,-------(4分)
设bn=an-2,则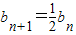 ,即{bn}是以b1=-1,
,即{bn}是以b1=-1, 为公比的等比数列,
为公比的等比数列,
所以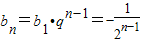 ,------------------(7分)
,------------------(7分)
所以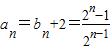 .-----------------(8分)
.-----------------(8分)
点评:本题考查数列的递推关系式的应用,数列通项公式的求法,猜想必须利用数学归纳法证明.
 an+1.利用n=2,3,4,即可求出a2,a3,a4.
an+1.利用n=2,3,4,即可求出a2,a3,a4.(2)解法一:通过(1)猜想数列的通项公式,然后利用数学归纳法证明;
解法二:构造{bn}是以b1=-1,
 为公比的等比数列,求出bn然后求数列{an}的通项公式.
为公比的等比数列,求出bn然后求数列{an}的通项公式.解答:解:(1)因为
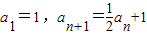 ,
,所以
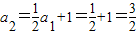 ,
,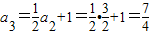 ,
,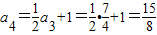 .-------------------(3分)
.-------------------(3分)(2)解法一:猜想:
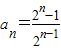 .下面用数学归纳法证明,
.下面用数学归纳法证明,证明:(1)当n=1时,
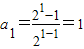 ,满足上式,显然成立;-------------------(4分)
,满足上式,显然成立;-------------------(4分)(2)假设当n=k时
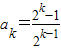 ,那么当n=k+1时,
,那么当n=k+1时,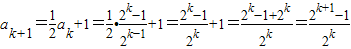 满足上式,
满足上式,即当n=k+1时猜想也成立.-------------------(7分)
由(1)(2)可知,对于n∈n*都有
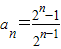 .------------------(8分)
.------------------(8分)解法二:因为
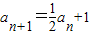 ,所以
,所以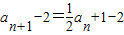 ,即
,即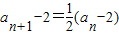 ,-------(4分)
,-------(4分)设bn=an-2,则
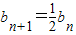 ,即{bn}是以b1=-1,
,即{bn}是以b1=-1, 为公比的等比数列,
为公比的等比数列,所以
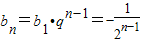 ,------------------(7分)
,------------------(7分) 所以
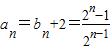 .-----------------(8分)
.-----------------(8分)点评:本题考查数列的递推关系式的应用,数列通项公式的求法,猜想必须利用数学归纳法证明.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目