题目内容
已知数列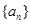 满足
满足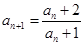 ,且
,且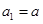 ,
,
(1)当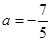 时,求出数列
时,求出数列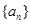 的所有项;
的所有项;
(2)当 时,设
时,设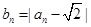 ,证明:
,证明: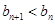 ;
;
(3)设(2)中的数列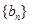 的前
的前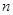 项和为
项和为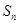 ,证明:
,证明: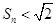 .
.
【答案】
(1) ,
, ,
, ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】
试题分析:(1)先将 代入找出递推公式,逐一求出数列的每一项;(2)通过式子的变形找出
代入找出递推公式,逐一求出数列的每一项;(2)通过式子的变形找出 的形式,利用放缩法比较大小;(3)放缩法求出解析式,再利用等比数列得求和公式求和.
的形式,利用放缩法比较大小;(3)放缩法求出解析式,再利用等比数列得求和公式求和.
试题解析: (1)证明:∵ ,
, ,
,
∴ ,
, ,
,
由于当 时,使递推式右边的分母为零。
时,使递推式右边的分母为零。
∴数列 只有三项:
只有三项: .
(3分)
.
(3分)
(2) ,
, 易知:
易知: ,
,
又
 ,
,
∴ (5分)
(5分)
由



 ,
,

即 (8分)
(8分)
(3)由(2)知:  ,
,
∴
∵ ,
,
∴ (11分)
(11分)

 ,
,
∴ (13分)
(13分)
考点:1.由递推公式求数列的每一项;2.放缩法比较大小;3.等比数列求和.

练习册系列答案
相关题目
 满足
满足 ,且
,且 (
( )
) ,
, ,
, (2)由(1)猜想
(2)由(1)猜想 ;
; 满足
满足 ,且
,且 (
( )。
)。 、
、 、
、 的值;
的值; 满足
满足 ,且
,且 (n
(n 2且n∈N*).
2且n∈N*). 的通项公式;(5分)
的通项公式;(5分) ,求
,求 ,并证明:
,并证明: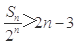 .(7分)
.(7分) 满足
满足 ,且
,且 ,且
,且 ,则数列
,则数列
 B.
B. C.
C. D.
D.