题目内容
【题目】已知圆![]() 与抛物线
与抛物线![]() 有一条斜率为1的公共切线
有一条斜率为1的公共切线![]() .
.
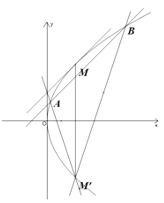
(1)求![]() .
.
(2)设![]() 与抛物线切于点
与抛物线切于点![]() ,作点
,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,在区域
,在区域![]() 内过
内过![]() 作两条关于直线
作两条关于直线![]() 对称的抛物线的弦
对称的抛物线的弦![]() ,
,![]() .连接
.连接![]() .
.
①求证:![]() ;
;
②设![]() 面积为
面积为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,(2)①证明见解析,②
,(2)①证明见解析,②![]()
【解析】
(1)设切线为![]() ,其与圆相切,列方程可得可得
,其与圆相切,列方程可得可得![]() 的值,又与抛物线相切,与抛物线联立,
的值,又与抛物线相切,与抛物线联立,![]() ,结合
,结合![]() ,可求出
,可求出![]() 的值;
的值;
(2)①由(1)可得切点为![]() ,故
,故![]() ,设直线
,设直线![]() 方程为
方程为![]() ,点
,点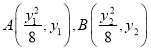 ,代入点的坐标可得
,代入点的坐标可得![]() 利用
利用![]() 与
与![]() 关于
关于![]() 对称得到
对称得到![]() ,联立
,联立![]() 与抛物线方程,结合韦达定理,可得
与抛物线方程,结合韦达定理,可得![]() ,即可证明
,即可证明![]() ;②求出
;②求出![]() 以及
以及![]() 到
到![]() 的距离,表示出
的距离,表示出![]() ,利用导数求其最值即可.
,利用导数求其最值即可.
(1)设切线为![]() .
.
∵直线与圆相切
∴![]() ,
,
解得![]() 或
或![]() ,
,
联立![]() ,
,
得![]() ,
,
由![]() ,得
,得![]() .
.
结合![]() 可知:
可知:![]() ,
,![]() ;
;
(2)①由上述方程知直线与抛物线的切点为![]() ,故
,故![]() ,
,
设直线![]() 方程为
方程为![]() ,点
,点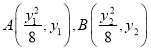
∴![]() ①
①
∵![]() 与
与![]() 关于
关于![]() 对称
对称
∴![]()
即:![]() ②
②
联立![]() 与抛物线方程,
与抛物线方程,
![]() ,化简整理得:
,化简整理得:![]()
![]()
∴![]() ,
,![]() ,
,![]() ,
,
代入②式整理得![]() ,
,
∴ ![]() ;
;

②由①知,![]() 方程为
方程为![]() ,
,
结合条件及![]() 可知
可知![]() ,
,
又![]()
![]() 到
到![]() 的距离
的距离![]()
∴![]() .
.
考虑![]() 其中
其中![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
此时![]() 的最大值为:
的最大值为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目