题目内容
(本题14分)设定义在R上的函数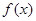 ,对任意
,对任意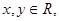 有
有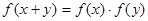 , 且当
, 且当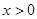 时,恒有
时,恒有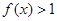 ,若
,若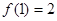 .
.
(1)求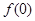 ;
;
(2)求证: 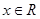 时
时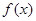 为单调递增函数.
为单调递增函数.
(3)解不等式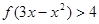 .
.
【答案】
(1) 或
或
(2) 为单调递增函数
为单调递增函数
(3)不等式解集为(1,2).
【解析】解:(1)令 或
或 ,
,
又 =
= ,故
,故 。
。
(2)由于 假设存在
假设存在 ,使
,使 ,则
,则
 ,与题设矛盾,所以
,与题设矛盾,所以 。
。
设 ,
, ,由已知
,由已知

 ,于是
,于是 为单调递增函数.
为单调递增函数.
(3)因为 ,不等式
,不等式 等价于
等价于 ,不等式解集为(1,2).
,不等式解集为(1,2).

练习册系列答案
相关题目
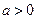 ,函数
,函数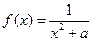 .
.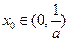 ,使
,使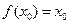 ;
; 义数列
义数列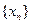 :
: ,
,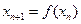 ,
,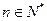 .
.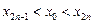 ;
;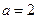 时,若
时,若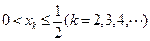 ,
,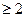 时,对任意
时,对任意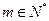 都有:
都有: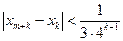
 ,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.
,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和. ,函数
,函数 .
. ,使
,使 ;
;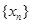 :
: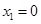 ,
, ,
,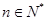 .
. ;
;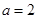 时, 若
时, 若 ,
, 时,对任意
时,对任意 都有:
都有: