题目内容
(本题满分14分)设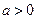 ,函数
,函数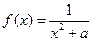 .
.
(Ⅰ)证明:存在唯一实数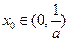 ,使
,使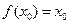 ;
;
(Ⅱ)定 义数列
义数列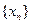 :
: ,
,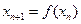 ,
,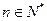 .
.
(i)求证:对任意正整数n都有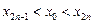 ;
;
(ii) 当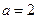 时,若
时,若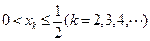 ,
,
证明:当k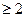 时,对任意
时,对任意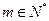 都有:
都有: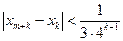
(Ⅰ)证明:略
解析

练习册系列答案
相关题目
题目内容
(本题满分14分)设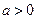 ,函数
,函数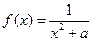 .
.
(Ⅰ)证明:存在唯一实数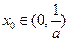 ,使
,使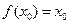 ;
;
(Ⅱ)定 义数列
义数列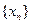 :
: ,
,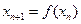 ,
,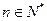 .
.
(i)求证:对任意正整数n都有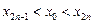 ;
;
(ii) 当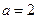 时,若
时,若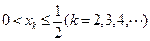 ,
,
证明:当k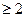 时,对任意
时,对任意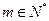 都有:
都有: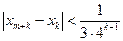
(Ⅰ)证明:略
解析
