题目内容
已知函数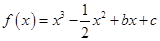 ,且
,且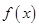 在
在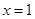 处取得极值.
处取得极值.
(1)求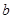 的值;
的值;
(2)若当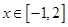 时,
时,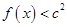 恒成立,求
恒成立,求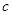 的取值范围;
的取值范围;
(3)对任意的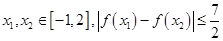 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
(1)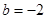 (2)
(2)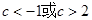 (3)不等式恒成立,证明:当
(3)不等式恒成立,证明:当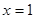 时,
时,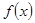 有极小值
有极小值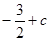 又
又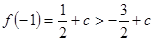 ∴
∴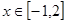 时,
时,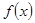 最小值为
最小值为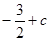
∴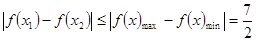 ,故结论成立.
,故结论成立.
解析试题分析:(1)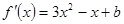
∵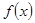 在
在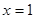 处取得极值,
处取得极值,
∴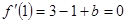
∴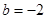 经检验,符合题意.
经检验,符合题意.
(2)∵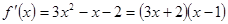

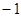
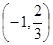
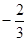




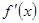


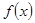
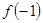

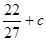

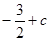

 练习册系列答案
练习册系列答案
阳光课堂口算题系列答案
快乐每一天神算手天天练系列答案
小学教材全解全析系列答案
原创讲练测课优新突破系列答案
学优冲刺100系列答案
名校秘题小学毕业升学系统总复习系列答案
名师面对面小考满分策略系列答案

课时练全优达标测试卷系列答案
万唯中考试题研究系列答案
相关题目


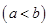 ,使得函数
,使得函数 的定义域、值域都是
的定义域、值域都是 ,若存在,则求出
,若存在,则求出 (
(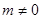 ),求
),求 的取值范围.
的取值范围. 是奇函数,
是奇函数, 是偶函数,并且
是偶函数,并且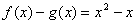 ,求
,求 ,设其定义域域是
,设其定义域域是 .
.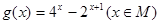 的值域.
的值域.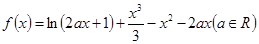
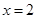 为
为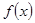 的极值点,求实数
的极值点,求实数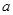 的值;
的值;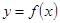 在
在 上为增函数,求实数
上为增函数,求实数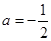 时,方程
时,方程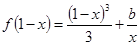 有实根,求实数
有实根,求实数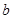 的最大值.
的最大值. 的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为
的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为 ,容积为
,容积为 .
.
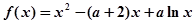 ,其中常数
,其中常数 。
。 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;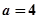 时,是否存在实数
时,是否存在实数 ,使得直线
,使得直线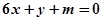 恰为曲线
恰为曲线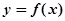 的切线?若存在,求出
的切线?若存在,求出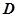 上的函数
上的函数 的图象在点
的图象在点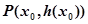 处的切线方程为
处的切线方程为 ,当
,当 时,若
时,若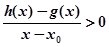 在
在 为函数
为函数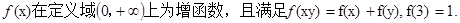
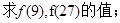

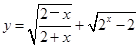 的定义域为
的定义域为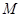 ,
, 时,求函数
时,求函数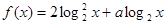 的最大值。
的最大值。