题目内容
11.已知集合A={x|1≤x≤4},f(x)=x2+px+q和g(x)=x+$\frac{4}{x}$是定义在A上的函数,且在x0处同时取到最小值,并满足f(x0)=g(x0).求f(x)在A上的最大值.分析 根据对勾函数的图象和性质,结合已知可得f(x)=x2+px+q在x=2时,取最小值4,进而求出p,q的值,结合二次函数的图象和性质,可得f(x)在A上的最大值.
解答 解:由对勾函数的图象和性质可得:
g(x)=x+$\frac{4}{x}$在x=2时,取最小值4,
故f(x)=x2+px+q在x=2时,也取最小值4,
故$-\frac{p}{2}$=2,$\frac{4q-{p}^{2}}{4}$=4,
解得:p=-4,q=8,
∴f(x)=x2-4x+8,
∴当x=4时,f(x)取最大值8.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
20.奇函数f(x)在(0,+∞)上满足:任意x1<x2,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,且f(2)=0,则不等式 $\frac{f(x)-f(-x)}{x}$<0的解集为( )
| A. | (-2,0)∪(0,2) | B. | (-∞,-2)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-2,0)∪(2,+∞) |
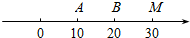 如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.