题目内容
正三角形ABC中D是BC上的点，∠ABD=60°，AB=4，BD=2，则
•
=
| AB |
| AD |
12
12
．分析：根据题意得AD是BC边上的中线，结合正三角形的性质得到AD是BC边上的高，即AD⊥BC，从而算出AD=2
且∠BAD=30°．再根据向量数量积的公式加以计算，可得
•
的值．
| 3 |
| AB |
| AD |
解答：解：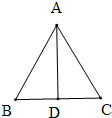
∵正△ABC中，BC上的点满足∠ABD=60°，AB=4，BD=2，
∴BD=
BC，可得AD是BC边上的中线，
因此AD是正△ABC的BC边上的高，即AD⊥BC，
∴∠BAD=90°-∠ABD=30°，AD=
=2
．
可得
•
=
•
•cos∠BAD=4×2
×cos30°=12．
故答案为：12
∵正△ABC中，BC上的点满足∠ABD=60°，AB=4，BD=2，∴BD=
| 1 |
| 2 |
因此AD是正△ABC的BC边上的高，即AD⊥BC，
∴∠BAD=90°-∠ABD=30°，AD=
| AB2-BD2 |
| 3 |
可得
| AB |
| AD |
| |AB| |
| |AD| |
| 3 |
故答案为：12
点评：本题在边长为4的等边三角形中求向量的数量积，着重考查了向量的数量积公式、正三角形的性质和勾股定理等知识，属于中档题．
练习册系列答案
相关题目
如图所示，在边长为4的正三角形ABC中，E，F依次是AB，AC的中点，AD⊥BC，EH⊥BC，FG⊥BC，D，H，G为垂足，若将△ABC绕AD旋转180°，求阴影部分形成的几何体的表面积．