题目内容
用定义证明:?(1)函数f(x)=ax+b(a<0,a、b为常数)在R上是减函数;?
(2)函数g(x)=![]() (k<0,k为常数)在(-∞,0)上是增函数.?
(k<0,k为常数)在(-∞,0)上是增函数.?
证明:(1)设任意的x1、x2∈R,且x1<x2,?
则f(x1)-f(x2)=(ax1+b)-(ax2+b)=a(x1-x2),?
由x1<x2及a<0,得a(x1-x2)>0.?
∴f(x1)-f(x2)>0,即f(x1)>f(x2).?
∴f(x)=ax+b(a<0)在R上为减函数.?
(2)设x1、x2∈(-∞,0),且x1<x2,则g(x1)-g(x2)=![]() -
-![]() =
=![]() ,?
,?
∵x1<x2<0,∴x1x2>0,x2-x1>0.?
又k<0,∴g(x1)-g(x2)<0,即g(x1)<g(x2).?
∴g(x)=![]() (k<0)在(-∞,0)上为增函数.?
(k<0)在(-∞,0)上为增函数.?
点评:证明或判断函数的单调性,严格地说必须用增、减函数定义,其步骤是:设出指定区间上的任意两个值→作差→变形→判符号→定结论.对于正、反比例函数,一、二次函数的单调性,要熟练掌握证明方法,并能结合图象快速指出单调区间.

练习册系列答案
相关题目
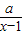 且此函数图象过点(2,1)
且此函数图象过点(2,1) 是定义域在(-1,1)上奇函数,且
是定义域在(-1,1)上奇函数,且 .
. 的解析式;
的解析式; .
. 是定义域在(-1,1)上的奇函数,且
是定义域在(-1,1)上的奇函数,且 .
. 的解析式;
的解析式; .
.