题目内容
 三棱锥D-ABC及其三视图中的主视图和左视图如图所示,则棱BD的长为
三棱锥D-ABC及其三视图中的主视图和左视图如图所示,则棱BD的长为4
| 2 |
4
.| 2 |
分析:由主视图知CD⊥平面ABC、B点在AC上的射影为AC中点及AC长,由左视图可知CD长及△ABC中变AC的高,利用勾股定理即可求出棱BD的长.
解答:解:由主视图知CD⊥平面ABC,设AC中点为E,则BE⊥AC,且AE=CE=2;
由左视图知CD=4,BE=2
,
在Rt△BCE中,BC=
=
=4,在Rt△BCD中,BD=
=
=4
.
故答案为:4
.
由左视图知CD=4,BE=2
| 3 |
在Rt△BCE中,BC=
| BE2+EC2 |
(2
|
| BC2+CD2 |
| 42+42 |
| 2 |
故答案为:4
| 2 |
点评:本题考查点、线、面间的距离计算,考查空间图形的三视图,考查学生的空间想象能力,考查学生分析解决问题的能力.

练习册系列答案
相关题目
 三棱锥D-ABC及其三视图中的正视图和左视图如图,则三棱锥中最长棱的长为( )
三棱锥D-ABC及其三视图中的正视图和左视图如图,则三棱锥中最长棱的长为( )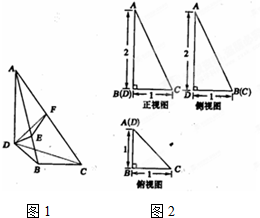 已知三棱锥A-BCD及其三视图如图所示.
已知三棱锥A-BCD及其三视图如图所示.




