题目内容
如图所示,中心均为原点O的双曲线与椭圆有公共焦点,M、N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则双曲线与椭圆的离心率的比值是( )
| A．3 | B．2 | C． | D． |
B
设椭圆的标准方程为
+
=1(a>b>0),半焦距为c1,
则椭圆的离心率为e1=
.
设双曲线的标准方程为
-
=1(m>0,n>0),半焦距为c2,
则双曲线的离心率为e2=
.
由双曲线与椭圆共焦点知c1=c2.
由点M,O,N将椭圆长轴四等分可知m=a-m,
即2m=a.
∴
=
=
=2.
故选B.
+=1(a>b>0),半焦距为c1,则椭圆的离心率为e1=
.设双曲线的标准方程为
-=1(m>0,n>0),半焦距为c2,则双曲线的离心率为e2=
.由双曲线与椭圆共焦点知c1=c2.
由点M,O,N将椭圆长轴四等分可知m=a-m,
即2m=a.
∴
===2.故选B.
练习册系列答案
教材全解字词句篇系列答案
相关题目
＝1(a>b>0)的左、右顶点，椭圆长半轴的长等于焦距，且直线x＝4是它的右准线．
上的动点，点
.线段PB的垂直平分线与半径PA相交于点M，记点M的轨迹为Γ.
时，求点M的坐标.
、
（
）连线的斜率之积等于非零常数m的点的轨迹，加上
、
两点所成的曲线C可以是圆、椭圆或双曲线．求曲线C的方程，并讨论C的形状与m值得关系．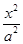
+
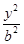=1(a>b>0)的两个焦点.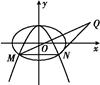
+
=1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
+
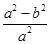
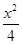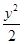=1的两个焦点是F1、F2,点P在该椭圆上,若|PF1|-|PF2|=2,则△PF1F2的面积是 .