题目内容
已知首项为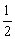 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知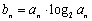 ,求数列{bn}的前n项和
,求数列{bn}的前n项和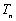 .
.
.解:(I)设等比数列{an}的公比为q,由题知a1= 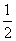 ,
,
又∵ S1+a1,S2+a2,S3+a3成等差数列,
∴ 2(S2+a2)=S1+a1+S3+a3,
变形得S2-S1+2a2=a1+S3-S2+a3,即得3a2=a1+2a3,
∴  q=
q=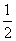 +q2,解得q=1或q=
+q2,解得q=1或q=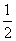 ,
,
又由{an}为递减数列,于是q=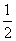 ,
,
∴ an=a1 =(
=( 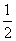 )n.
)n.
(Ⅱ)由于bn=anlog2an=-n∙( 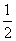 )n,
)n,
∴  ,
,
于是 ,
,
两式相减得:

整理得 .
.

练习册系列答案
相关题目
 与曲线
与曲线 有两个不同的交点,则
有两个不同的交点,则 的取值范围为 。
的取值范围为 。 =0,则△AOC的面积为
=0,则△AOC的面积为 B.
B. 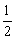 C.
C. D.
D.
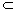 α,m
α,m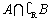 =
=
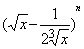 的展开式中第四项为常数项,则
的展开式中第四项为常数项,则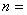
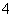 B.
B. 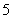 C.
C. 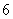 D.
D. 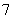
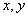 满足约束条件
满足约束条件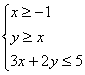 ,则
,则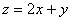 的最大值为( )
的最大值为( )