题目内容
已知△ABC的外接圆的圆心为O,半径为1,若 =0,则△AOC的面积为
=0,则△AOC的面积为
A. B.
B. 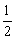 C.
C. D.
D.
A

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
题目内容
已知△ABC的外接圆的圆心为O,半径为1,若 =0,则△AOC的面积为
=0,则△AOC的面积为
A. B.
B. 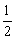 C.
C. D.
D.
A

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案