题目内容
已知函数 (
( 为常数,且
为常数,且 ).
).
(1)当 时,求函数
时,求函数 的最小值(用
的最小值(用 表示);
表示);
(2)是否存在不同的实数 使得
使得 ,
, ,并且
,并且 ,若存在,求出实数
,若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(1)令
当 即
即 时,
时, 
当 即
即 时,
时,
综上: .
.
(2)解法一:假设存在,则由已知得
 ,等价于
,等价于 在区间
在区间 上有两个不同的实根
上有两个不同的实根
令 ,则
,则 在
在 上有两个不同的零点
上有两个不同的零点

 .
.
解法2:假设存在,则由已知得

等价于 在区间
在区间 上有两个不同的实根
上有两个不同的实根
等价于 ,作出函数图象,可得
,作出函数图象,可得 .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
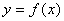 的图象与直线
的图象与直线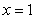 的交点个数为0或1;
的交点个数为0或1;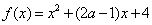 , 若当
, 若当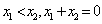 时,总有
时,总有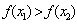 ,
,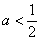 ;
;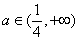 时,函数
时,函数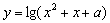 的值域为
的值域为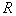 ;
;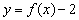 的图象关于点
的图象关于点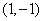 对称的图象对应的函数为
对称的图象对应的函数为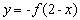 .
. 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数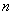 的最小值为________
的最小值为________ 是圆
是圆 上的三个点,
上的三个点, 的延长线与线段
的延长线与线段 交于圆内一点
交于圆内一点 ,若
,若 ,则( )
,则( ) B.
B. C.
C. D.
D.
 ,且
,且 .当
.当 时,函数
时,函数 ,
, ,则
,则 .
. 与
与 之间的距离为
之间的距离为  B.
B. C. 1 D.
C. 1 D. 
 ,那么命题“若
,那么命题“若 中至少有一个不为0,则
中至少有一个不为0,则 .”的逆否命题是 .
.”的逆否命题是 . 与圆
与圆 相交于M,N两点,若
相交于M,N两点,若 ,则k的取值范围是( )
,则k的取值范围是( ) B.
B.
 D.
D.