题目内容
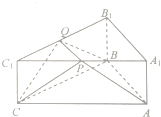 如图,ABC-A1B1C1是地面边长为2,高为
如图,ABC-A1B1C1是地面边长为2,高为
| ||
| 2 |
(1)证明:PQ∥A1B1;
(2)是否存在λ,使得平面CPQ⊥截面APQB?如果存在,求出λ的值;如果不存在,请说明理由.
考点:平面与平面垂直的判定,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)由正三棱柱的性质可知,上下两个底面平行,由两个平面平行的性质定理可得PQ∥AB,由此能证明PQ∥A1B1.
(2)假设存在这样的λ满足题设,分别取AB的中点D,PQ的中点E,连接DE,由已知得∠CED为二面角A-PQ-C的平面角,连接C1E并延长,交A1B1于F,若平面CPQ⊥截面APQB,则CE2+DE2=CD2,由此能求出λ=
.
(2)假设存在这样的λ满足题设,分别取AB的中点D,PQ的中点E,连接DE,由已知得∠CED为二面角A-PQ-C的平面角,连接C1E并延长,交A1B1于F,若平面CPQ⊥截面APQB,则CE2+DE2=CD2,由此能求出λ=
| 1 |
| 2 |
解答:
(1)证明:由正三棱柱的性质可知,上下两个底面平行,
且截面APQB∩上底面A1B1C1=PQ,截面APQB∩下底面ABC=AB,
由两个平面平行的性质定理可得PQ∥AB,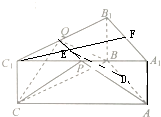
∴PQ∥A1B1.…(6分)
(2)解:假设存在这样的λ满足题设,
分别取AB的中点D,PQ的中点E,连接DE,
由(1)及正三棱柱的性质可知△CPQ为等腰三角形,APQB为等腰梯形,
∴CE⊥PQ,DE⊥PQ,
∴∠CED为二面角A-PQ-C的平面角,…(8分)
连接C1E并延长,交A1B1于F,
由(1)得,
=
=λ,C1A1=2,C1F=
,
∴C1E=
λ,EF=
(1-λ),…(9分)
在Rt△CC1E中,CE2=
+3λ2,在Rt△DFE中,DE2=
+(1-λ)2,
若平面CPQ⊥截面APQB,则∠CED=90°,
∴CE2+DE2=CD2,将以上数据代入整理,
得3λ2-3λ+
=0,解得λ=
.…(13分)
且截面APQB∩上底面A1B1C1=PQ,截面APQB∩下底面ABC=AB,
由两个平面平行的性质定理可得PQ∥AB,

∴PQ∥A1B1.…(6分)
(2)解:假设存在这样的λ满足题设,
分别取AB的中点D,PQ的中点E,连接DE,
由(1)及正三棱柱的性质可知△CPQ为等腰三角形,APQB为等腰梯形,
∴CE⊥PQ,DE⊥PQ,
∴∠CED为二面角A-PQ-C的平面角,…(8分)
连接C1E并延长,交A1B1于F,
由(1)得,
| C1P |
| C1A1 |
| C1E |
| C1F |
| 3 |
∴C1E=
| 3 |
| 3 |
在Rt△CC1E中,CE2=
| 3 |
| 4 |
| 3 |
| 4 |
若平面CPQ⊥截面APQB,则∠CED=90°,
∴CE2+DE2=CD2,将以上数据代入整理,
得3λ2-3λ+
| 3 |
| 4 |
| 1 |
| 2 |
点评:本题考查线线平行的证明,考查使得面面垂直的实数值是否存在的判断与求法,考查方程思想、等价转化思想等数学思想方法和学生的空间想象能力、逻辑推理能力和运算求解能力,是中档题.

练习册系列答案
相关题目
若a>0且a≠1,b>0,则“logab>0”是“(a一1)(b一1)>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
| π |
| 3 |
| A、3 | ||||
B、
| ||||
| C、2 | ||||
D、
|