题目内容
用二分法求方程x3-2x-5=0在区间[2,3]上的实根,取区间中点x0=2.5,则下一个有根区间是
- A.[2,2.5]
- B.[2.5,3]
- C.
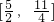
- D.以上都不对
A
分析:方程的实根就是对应函数f(x)的零点,由 f(2)<0,f(2.5)>0 知,f(x)零点所在的区间为[2,2.5].
解答:设f(x)=x3-2x-5,
f(2)=-1<0,f(3)=16>0,
f(2.5)=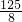 -10=
-10=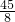 >0,
>0,
f(x)零点所在的区间为[2,2.5],
方程x3-2x-5=0有根的区间是[2,2.5],
故选A.
点评:本题考查用二分法求方程的根所在的区间的方法,方程的实根就是对应函数f(x)的零点,函数在区间上存在零点的条件是函数在区间的端点处的函数值异号.
分析:方程的实根就是对应函数f(x)的零点,由 f(2)<0,f(2.5)>0 知,f(x)零点所在的区间为[2,2.5].
解答:设f(x)=x3-2x-5,
f(2)=-1<0,f(3)=16>0,
f(2.5)=
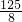 -10=
-10=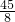 >0,
>0,f(x)零点所在的区间为[2,2.5],
方程x3-2x-5=0有根的区间是[2,2.5],
故选A.
点评:本题考查用二分法求方程的根所在的区间的方法,方程的实根就是对应函数f(x)的零点,函数在区间上存在零点的条件是函数在区间的端点处的函数值异号.

练习册系列答案
相关题目