题目内容
(本小题满分12分)
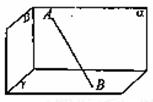
在四棱锥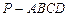 中,底面
中,底面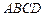 是一直角梯形,
是一直角梯形,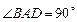 ,
,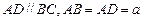 ,
,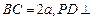 底面
底面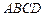 .
.
(1)在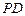 上是否存在一点
上是否存在一点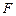 ,使得
,使得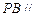 平面
平面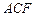 ,若存在,求出
,若存在,求出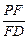 的值;
的值;
若不存在,试说明理由;
(2)在(1)的条件下,若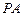 与
与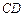 所成的角为
所成的角为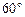 ,求二面角
,求二面角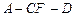 的余弦值.
的余弦值.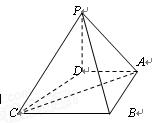
在四棱锥
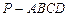 中,底面
中,底面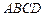 是一直角梯形,
是一直角梯形,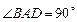 ,
,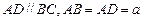 ,
,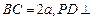 底面
底面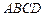 .
.(1)在
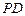 上是否存在一点
上是否存在一点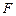 ,使得
,使得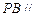 平面
平面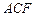 ,若存在,求出
,若存在,求出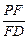 的值;
的值;若不存在,试说明理由;
(2)在(1)的条件下,若
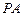 与
与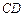 所成的角为
所成的角为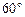 ,求二面角
,求二面角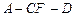 的余弦值.
的余弦值.
(1) ,理由见解析。
,理由见解析。
(2)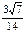
 ,理由见解析。
,理由见解析。(2)
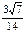
(1)方法一:存在点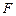 使
使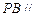 平面
平面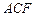 ,
, …………………………1分
…………………………1分
连接 交
交 于
于 ,连接
,连接 ,
,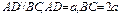 ,所以
,所以 ,所以
,所以 …4分
…4分
又 平面
平面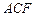 ,
, 不在平面
不在平面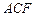 内,所以
内,所以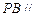 平面
平面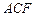 …………………………5分
…………………………5分
方法二:建立如图所示的空间直角坐标系, ,
, ,
, ,
, ,…1分
,…1分
设 ,则
,则 ,假设存在点
,假设存在点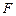 使
使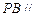 平面
平面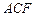 ,
, ………2分
………2分
设平面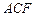 的一个法向量为
的一个法向量为 ,
, ,
,
 ,
, ,所以
,所以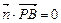 ,
, ……4分所以
……4分所以 ……5分
……5分
(2) ,
, ,因为
,因为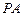 与
与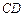 所成的角为
所成的角为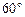
所以 ,则
,则 ……………7分
……………7分
由(1)知平面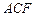 的一个法向量为
的一个法向量为 …………………………8分
…………………………8分
因为 ,
, ,所以
,所以
所以 ,所以
,所以 ,又
,又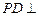 底面
底面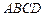 ,则
,则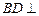 平面
平面 ,
,
所以 是平面
是平面 的一个法向量…………………………10分
的一个法向量…………………………10分
所以 ,所以二面角的余弦值为
,所以二面角的余弦值为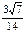 …………12分
…………12分
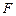 使
使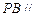 平面
平面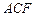 ,
, …………………………1分
…………………………1分连接
 交
交 于
于 ,连接
,连接 ,
,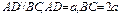 ,所以
,所以 ,所以
,所以 …4分
…4分又
 平面
平面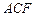 ,
, 不在平面
不在平面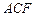 内,所以
内,所以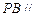 平面
平面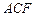 …………………………5分
…………………………5分方法二:建立如图所示的空间直角坐标系,
 ,
, ,
, ,
, ,…1分
,…1分设
 ,则
,则 ,假设存在点
,假设存在点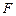 使
使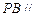 平面
平面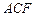 ,
, ………2分
………2分设平面
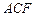 的一个法向量为
的一个法向量为 ,
, ,
,
 ,
, ,所以
,所以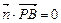 ,
, ……4分所以
……4分所以 ……5分
……5分(2)
 ,
, ,因为
,因为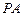 与
与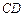 所成的角为
所成的角为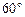
所以
 ,则
,则 ……………7分
……………7分由(1)知平面
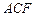 的一个法向量为
的一个法向量为 …………………………8分
…………………………8分因为
 ,
, ,所以
,所以
所以
 ,所以
,所以 ,又
,又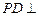 底面
底面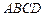 ,则
,则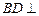 平面
平面 ,
,所以
 是平面
是平面 的一个法向量…………………………10分
的一个法向量…………………………10分所以
 ,所以二面角的余弦值为
,所以二面角的余弦值为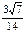 …………12分
…………12分
练习册系列答案
相关题目
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.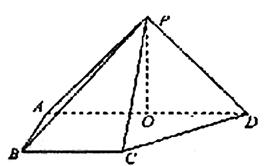
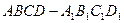 中,
中,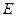 、
、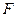 分别
分别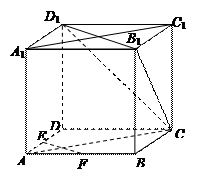
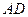 、
、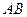 的中点.(1)求证:
的中点.(1)求证: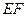 ∥平面
∥平面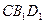 ;
;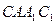 ⊥平面
⊥平面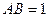 ,一个动点从点
,一个动点从点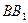 、
、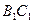 、
、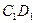 、
、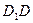 、
、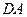 上的点,
上的点, 中,指出
中,指出 ,
, 所在直线与各个面的关系.
所在直线与各个面的关系.
 ,
, ,平面
,平面 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,点
,点 在线段
在线段 上。
上。 平面
平面 为何值时,
为何值时, ∥平面
∥平面 ?写出结论,并加以证明;
?写出结论,并加以证明;
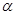 、
、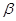 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面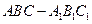 中,侧棱长为
中,侧棱长为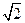 ,底面三角形的边长为1,则
,底面三角形的边长为1,则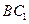 与侧面
与侧面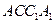 所成的角是____________
所成的角是____________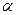 、
、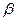 、
、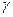 两两互相垂直,长为
两两互相垂直,长为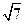 的线段AB在
的线段AB在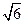 、a、b,则
、a、b,则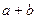 的最大值为 。
的最大值为 。