题目内容
已知函数
(1)求函数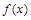 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)求函数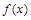 单调递增区间;
单调递增区间;
(3)若
 ∈[1,1],使得
∈[1,1],使得 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围.
(1)函数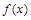 在点
在点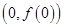 处的切线方程为
处的切线方程为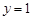 ;(2)函数
;(2)函数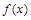 单调递增区间
单调递增区间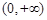 ;
;
(3)实数a的取值范围是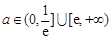 .
.
解析试题分析:⑴ 先根据函数解析式求出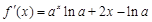 ,把
,把 代入求出斜率,进而求得切线方程;⑵ 因为当
代入求出斜率,进而求得切线方程;⑵ 因为当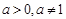 时,总有
时,总有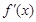 在
在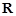 上是增函数, 又
上是增函数, 又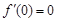 ,所以函数
,所以函数 的单调增区间为
的单调增区间为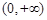 ;⑶ 要使
;⑶ 要使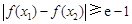 成立,只需
成立,只需 成立即可;再分
成立即可;再分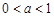 和
和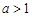 两种情况讨论即可.
两种情况讨论即可.
试题解析:⑴ 因为函数 ,
,
所以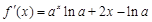 ,
,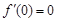 , 2分
, 2分
又因为 ,所以函数
,所以函数 在点
在点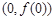 处的切线方程为
处的切线方程为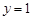 . 4分
. 4分
⑵ 由⑴,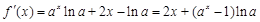 .
.
因为当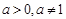 时,总有
时,总有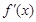 在
在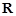 上是增函数,
上是增函数,
又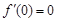 ,所以不等式
,所以不等式 的解集为
的解集为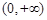 ,
,
故函数 的单调增区间为
的单调增区间为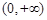 8分
8分
⑶ 因为存在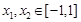 ,使得
,使得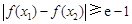 成立,
成立,
而当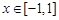 时,
时, ,
,
所以只要 即可 9分
即可 9分
又因为 ,
,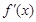 ,
, 的变化情况如下表所示:
的变化情况如下表所示:


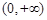
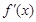


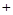

减函数 极小值  练习册系列答案
练习册系列答案
学业水平考试全景训练系列答案
正宗十三县系列答案
中考专题分类集训系列答案

完美读法系列答案
美文赏读系列答案
必考点灵通复习法系列答案
名校调研系列卷每周一考系列答案
同步解析与测评初中总复习指导与训练系列答案
专题分类卷系列答案
相关题目
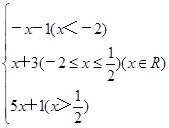 .
. x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)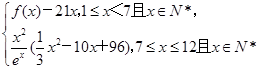
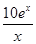 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)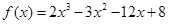 .
. 的单调区间;
的单调区间;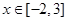 ,求函数
,求函数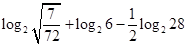 ;
;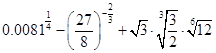 .
.
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
 满足条件
满足条件 时,对于
时,对于 ,
,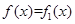 ;
; 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若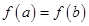 ,求函数
,求函数 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)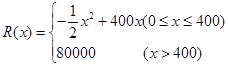 ,其中
,其中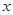 是组合床柜的月产量.
是组合床柜的月产量. 元表示为月产量
元表示为月产量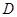 (分贝)由公式
(分贝)由公式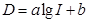 (
(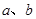 为非零常数)给出,其中
为非零常数)给出,其中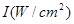 为声音能量.
为声音能量.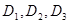 满足
满足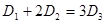 时,求对应的声音能量
时,求对应的声音能量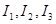 满足的等量关系式;
满足的等量关系式; 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为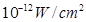 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.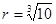 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.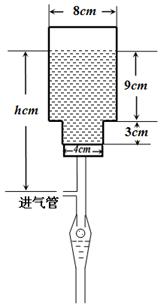
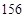 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?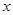 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为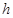 (单位:厘米),已知当
(单位:厘米),已知当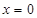 时,
时,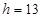 .试将
.试将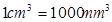 )
)