题目内容
在直角坐标平面xOy中,已知点A(3,2),点B在圆x2+y2=1上运动,动点P满足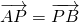 ,则点P的轨迹是
,则点P的轨迹是
- A.圆
- B.椭圆
- C.抛物线
- D.直线
A
分析:首先设出P、B点的坐标,然后根据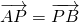 ,得出x1=2x-3,y1=2y-2,再将P点坐标代入圆的方程即可得出答案.
,得出x1=2x-3,y1=2y-2,再将P点坐标代入圆的方程即可得出答案.
解答:设P(x,y),B(x1,y1)
∵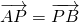 ,
,
即(x-3,y-2)=(x1-x,y1-y)
∴x1=2x-3,y1=2y-2
∵点B在圆x2+y2=1上运动
∴(2x-3)2+(2y-2)2=1
∴点P的轨迹是圆
故选A.
点评:本题考查了轨迹方程以及圆的方程,解题的关键是根据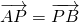 求出p点坐标,比较容易.
求出p点坐标,比较容易.
分析:首先设出P、B点的坐标,然后根据
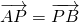 ,得出x1=2x-3,y1=2y-2,再将P点坐标代入圆的方程即可得出答案.
,得出x1=2x-3,y1=2y-2,再将P点坐标代入圆的方程即可得出答案.解答:设P(x,y),B(x1,y1)
∵
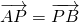 ,
,即(x-3,y-2)=(x1-x,y1-y)
∴x1=2x-3,y1=2y-2
∵点B在圆x2+y2=1上运动
∴(2x-3)2+(2y-2)2=1
∴点P的轨迹是圆
故选A.
点评:本题考查了轨迹方程以及圆的方程,解题的关键是根据
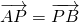 求出p点坐标,比较容易.
求出p点坐标,比较容易. 
练习册系列答案
相关题目