Question

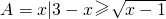，B={x||x-1|＞a，a＞0}若A∩B=∅，求a的取值范围．

Answer 1

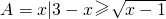解：由可得
∴A={x|1≤x≤2}
又由B={x||x-1|＞a，a＞0}
可得x-1≥a或x-1≤-a，
即x≥1+a或x≤1-a，
因为A∩B=∅，画数轴如图：
由图可知，1+a≥2且1-a≤1，所以，得a≥1
分析：先分别化简集合A，B，再根据A∩B=∅，借助于数轴，构建不等式，从而可求a的取值范围．
点评：本题重点考查集合的运算，考查解不等式，解题的关键是利用A∩B=∅，画数轴结论不等式．