题目内容
【题目】已知椭圆
过点
且椭圆的短轴长为
.
（Ⅰ）求椭圆
的方程；
（Ⅱ）已知动直线
过右焦点
，且与椭圆分别交于
两点.试问
轴上是否存在定点
，使得，
恒成立？若存在求出点的坐标；若不存在，说明理由.
【答案】（Ⅰ）
（Ⅱ）存在，
【解析】
（Ⅰ）由椭圆性质可知
,点代入即可求得结果.
（Ⅱ）假设存在定点
符合题意，①当直线
的斜率不存在时，由
解得
或
；②当直线的斜率为0时,解得
或.由①②可得,然后证明当时,通过方程联立,借助韦达定理,坐标表示即可证得结论.
解：（Ⅰ）因为椭圆
过点
，所以
.
又椭圆的短轴长为
，所以，所以
，
解得
.
所以椭圆的方程为.
（Ⅱ）假设在
轴上存在定点，使得，
①当直线的斜率不存在时，则
，
，
，
由
，解得或；
②当直线的斜率为0时，则
，
，
，
由
，解得或.
由①②可得，即点
的坐标为
.
下面证明当时，恒成立，当直线的斜率不存在或斜率为0时，由①②知结论成立.
当直线斜率存在且不为0时，设其方程为
，
，
，
由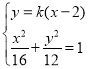
，得
，
直线经过椭圆内一点，一定与椭圆有两个交点，
且
，
.
，
所以
.
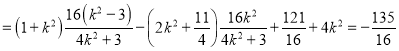综上所述，在轴上存在定点，使得恒成立..
练习册系列答案
相关题目
