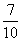题目内容
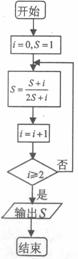
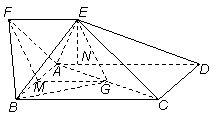
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD//FE,∠AFE=60º,且平面ABCD⊥平面ADEF,AF=FE=AB=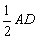 =2,点G为AC的中点.
=2,点G为AC的中点.
(Ⅰ)求证:EG//平面ABF;
(Ⅱ)求三棱锥B-AEG的体积;
(Ⅲ)试判断平面BAE与平面DCE是否垂直?若垂直,请证明;若不垂直,请说明理由.
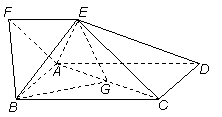
(I)证明:取AB中点M,连FM,GM.
∵ G为对角线AC的中点,
∴ GM∥AD,且GM=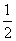 AD,
AD,
又∵ FE∥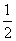 AD,
AD,
 ∴ GM∥FE且GM=FE.
∴ GM∥FE且GM=FE.
∴四边形GMFE为平行四边形,即EG∥FM.
又∵ 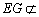 平面ABF,
平面ABF,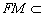 平面ABF,
平面ABF,
∴ EG∥平面ABF.
(Ⅱ)解:作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED ,面ABCD∩面AFED=AD,
得EN⊥平面ABCD,即EN为三棱锥E-ABG的高.
∵ 在△AEF中,AF=FE,∠AFE=60º,
∴ △AEF是正三角形.
∴ ∠AEF=60º,
由EF//AD知∠EAD=60º,
∴ EN=AE∙sin60º=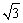 .
.
∴ 三棱锥B-AEG的体积为
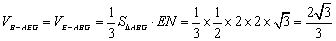 .
.
(Ⅲ)解:平面BAE⊥平面DCE.证明如下:
∵ 四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴ CD⊥平面AFED,
∴ CD⊥AE.
∵ 四边形AFED为梯形,FE∥AD,且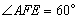 ,
,
∴ 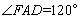 .
.
又在△AED中,EA=2,AD=4,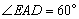 ,
,
由余弦定理,得ED=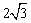 .
.
∴ EA2+ED2=AD2,
∴ ED⊥AE.
又∵ ED∩CD=D,
∴ AE⊥平面DCE,
又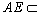 面BAE,
面BAE,
∴ 平面BAE⊥平面DCE.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 在圆C:
在圆C: 上运动,则动点
上运动,则动点 的轨迹方程是_______________
的轨迹方程是_______________ (
( 是虚数单位)是纯虚数,则实数
是虚数单位)是纯虚数,则实数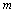 的值为 .
的值为 . B.8+
B.8+ C.8+
C.8+ D.8+
D.8+

 =4,则输出结果为
=4,则输出结果为

 >
> 成立,则实数m的取值范围为
成立,则实数m的取值范围为 B.
B. C.
C. D.
D.
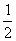 B.
B.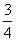 C.
C. D.
D.