题目内容
已知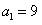 ,点
,点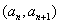 在函数
在函数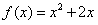 的图象上,其中n∈N*,设
的图象上,其中n∈N*,设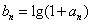 。
。
(Ⅰ)证明数列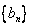 是等比数列;
是等比数列;
(Ⅱ)设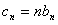 ,求数列
,求数列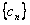 的前n项和
的前n项和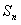 ;
;
(Ⅲ)设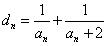 ,求数列
,求数列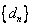 的前n项和
的前n项和 。
。
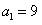 ,点
,点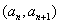 在函数
在函数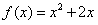 的图象上,其中n∈N*,设
的图象上,其中n∈N*,设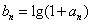 。
。(Ⅰ)证明数列
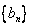 是等比数列;
是等比数列;(Ⅱ)设
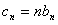 ,求数列
,求数列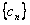 的前n项和
的前n项和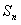 ;
;(Ⅲ)设
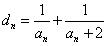 ,求数列
,求数列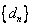 的前n项和
的前n项和 。
。 (Ⅰ)证明:由题意,知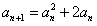 ,
,
∴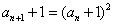 ,
,
又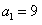 ,
,
∴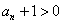 ,
,
∴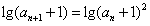 ,
,
即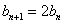 ,
,
又∵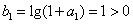 ,
,
∴数列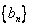 是公比为2的等比数列。
是公比为2的等比数列。
(Ⅱ)解:由(Ⅰ)知,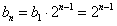 ,
,
∴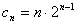 ,
,
∴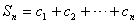
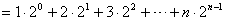 ,
,
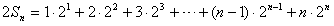 ,
,
两式相减,得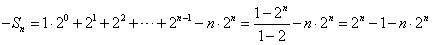 ,
,
∴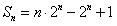 。
。
(Ⅲ)解:∵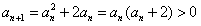 ,
,
∴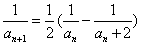 ,
,
∴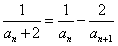 ,
,
∴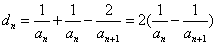 ,
,
∴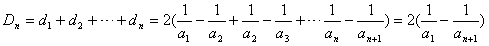 ,
,
又由(Ⅰ)知,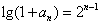 ,
,
∴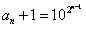 ,
,
∴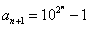 ,
,
∴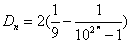 。
。
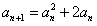 ,
,∴
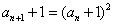 ,
,又
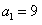 ,
,∴
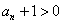 ,
,∴
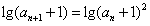 ,
,即
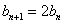 ,
,又∵
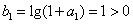 ,
,∴数列
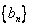 是公比为2的等比数列。
是公比为2的等比数列。(Ⅱ)解:由(Ⅰ)知,
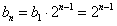 ,
,∴
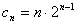 ,
,∴
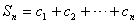
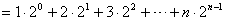 ,
,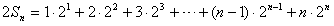 ,
,两式相减,得
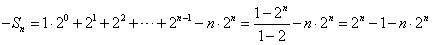 ,
,∴
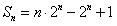 。
。(Ⅲ)解:∵
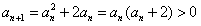 ,
,∴
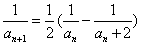 ,
,∴
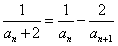 ,
,∴
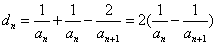 ,
,∴
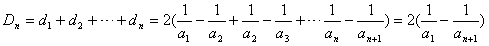 ,
,又由(Ⅰ)知,
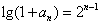 ,
,∴
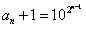 ,
,∴
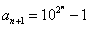 ,
,∴
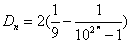 。
。
练习册系列答案
相关题目
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
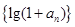 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 及数列
及数列 的通项;
的通项; ,求数列
,求数列 的前
的前 项和
项和 。
。 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; 的前
的前 项积为
项积为 ,求
,求 的通项公式;
的通项公式; 是
是 与
与 的等差中项,数列
的等差中项,数列 的前
的前 ,求证:
,求证: .
.
 ,点
,点 在函数
在函数 的图象上,其中
的图象上,其中
 是等比数列;
是等比数列; ,求
,求 ;
; ,求数列
,求数列 的前n项和为Sn,并证明Sn<1
的前n项和为Sn,并证明Sn<1