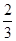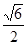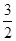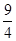题目内容
设数列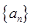 的前项和为
的前项和为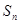 ,且
,且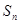
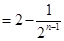 ,
,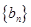 为等差数列,且
为等差数列,且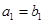 ,
,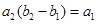
(Ⅰ)求数列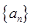 和
和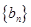 通项公式;
通项公式;
(Ⅱ)设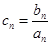 ,求数列
,求数列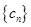 的前
的前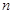 项和
项和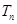 .
.
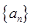 的前项和为
的前项和为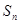 ,且
,且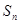
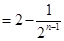 ,
,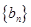 为等差数列,且
为等差数列,且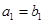 ,
,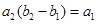
(Ⅰ)求数列
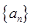 和
和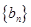 通项公式;
通项公式;(Ⅱ)设
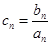 ,求数列
,求数列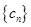 的前
的前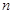 项和
项和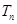 .
.(Ⅰ)  ,
, (Ⅱ)
(Ⅱ) 
 ,
, (Ⅱ)
(Ⅱ) 
本题考查Sn与an关系的具体应用,指数的运算,数列错位相消法求和知识和方法.要注意对n的值进行讨论
(Ⅰ)当 时,
时, .
.
当 时,
时, ,此式对
,此式对 也成立.
也成立.

 . ,从而
. ,从而 ,
, .又因为
.又因为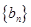 为等差数列,
为等差数列, 公差
公差 ,得到通项公式。
,得到通项公式。
(2)由(1)可知
,然后利用错位相减法得到求和。
解:(1)当 时,
时, .
.
当 时,
时, ,此式对
,此式对 也成立.
也成立.

 . ,从而
. ,从而 ,
, .
.
又因为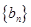 为等差数列,
为等差数列, 公差
公差 ,
,  .
.
(2)由(1)可知 ,
,
所以 . ①①
. ①① 2得
2得
 . ②
. ②
①-②得:


 .
.
 .
.
(Ⅰ)当
 时,
时, .
.当
 时,
时, ,此式对
,此式对 也成立.
也成立.
 . ,从而
. ,从而 ,
, .又因为
.又因为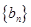 为等差数列,
为等差数列, 公差
公差 ,得到通项公式。
,得到通项公式。(2)由(1)可知

,然后利用错位相减法得到求和。
解:(1)当
 时,
时, .
.当
 时,
时, ,此式对
,此式对 也成立.
也成立.
 . ,从而
. ,从而 ,
, .
.又因为
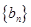 为等差数列,
为等差数列, 公差
公差 ,
,  .
.(2)由(1)可知
 ,
,所以
 . ①①
. ①① 2得
2得 . ②
. ②①-②得:



 .
. .
.
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
, (
(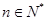 ).
). 是等比数列,求出数列
是等比数列,求出数列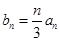 ,求数列
,求数列 的前
的前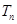 ;
;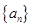 中,
中,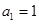 ,
, .
.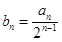 .证明:数列
.证明:数列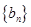 是等差数列;
是等差数列;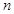 项和
项和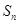 .
.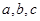 成等比数列,
成等比数列,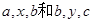 分别成等差数列,且
分别成等差数列,且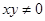 ,则
,则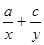 的值等于( )
的值等于( )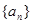 ,
,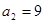 ,
,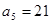 ,
,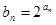 ,求数列
,求数列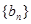 的前
的前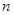 项和
项和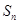 。
。 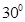 B、
B、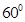 C、
C、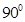 D、
D、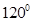
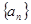 满足
满足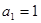 ,
,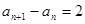 ;数列
;数列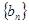 满足
满足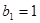 ,
,
 和
和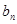 的通项公式
的通项公式 的前
的前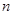 项和
项和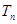
 中,
中,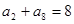 ,则该数列前9项和
,则该数列前9项和
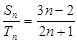 , 则
, 则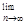
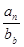 的值是
的值是