题目内容
 如图,△ABC是正三角形,EA和DC都垂直于平面ABC且EA=AB=2a,DC=a,F,G,H分别是EB,AB和BC的中点.求证:
如图,△ABC是正三角形,EA和DC都垂直于平面ABC且EA=AB=2a,DC=a,F,G,H分别是EB,AB和BC的中点.求证:(1)FG∥平面AEDC;
(2)平面AEDC∥平面FGH
(3)FD∥平面ABC.
分析:(1)证FG∥平面AEDC,只要证明FG∥AE,且AE?平面AEDC,FG?平面AEDC即可;
(2)证平面AEDC∥平面FGH,只要证明平面FGH内的FG∥平面AEDC,GH∥平面AEDC,且FG∩GH=G即可;
(3)证FD∥平面ABC,只要证明FD∥GC,且FD?平面ABC,GC?平面ABC即可,由FG∥DC,且FG=DC,得四边形FGCD是平行四边形,可证得.
(2)证平面AEDC∥平面FGH,只要证明平面FGH内的FG∥平面AEDC,GH∥平面AEDC,且FG∩GH=G即可;
(3)证FD∥平面ABC,只要证明FD∥GC,且FD?平面ABC,GC?平面ABC即可,由FG∥DC,且FG=DC,得四边形FGCD是平行四边形,可证得.
解答: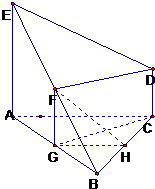 证明:(1)∵F,G分别是EB,AB的中点,∴FG为△EAB的中位线,∴FG∥AE;
证明:(1)∵F,G分别是EB,AB的中点,∴FG为△EAB的中位线,∴FG∥AE;
又AE?平面AEDC,FG?平面AEDC,
∴FG∥平面AEDC;
(2)∵G,H分别是AB和BC的中点,∴HG为△CAB的中位线,∴HG∥AC;
又AC?平面AEDC,HG?平面AEDC,∴GH∥平面AEDC;
由(1)得FG∥平面AEDC,且FG∩GH=G,FG?平面FGH,GH?平面FGH;
∴平面AEDC∥平面FGH;
(3)∵FG为△EAB的中位线,∴FG=
AE=a,且FG∥EA;
∵EA⊥平面ABC,DC⊥平面ABC,∴EA∥DC;
∴FG∥DC,又FG=DC=a,
∴四边形FGCD是平行四边形,
∴FD∥GC,又FD?平面ABC,GC?平面ABC,
∴FD∥平面ABC.
 证明:(1)∵F,G分别是EB,AB的中点,∴FG为△EAB的中位线,∴FG∥AE;
证明:(1)∵F,G分别是EB,AB的中点,∴FG为△EAB的中位线,∴FG∥AE;又AE?平面AEDC,FG?平面AEDC,
∴FG∥平面AEDC;
(2)∵G,H分别是AB和BC的中点,∴HG为△CAB的中位线,∴HG∥AC;
又AC?平面AEDC,HG?平面AEDC,∴GH∥平面AEDC;
由(1)得FG∥平面AEDC,且FG∩GH=G,FG?平面FGH,GH?平面FGH;
∴平面AEDC∥平面FGH;
(3)∵FG为△EAB的中位线,∴FG=
| 1 |
| 2 |
∵EA⊥平面ABC,DC⊥平面ABC,∴EA∥DC;
∴FG∥DC,又FG=DC=a,
∴四边形FGCD是平行四边形,
∴FD∥GC,又FD?平面ABC,GC?平面ABC,
∴FD∥平面ABC.
点评:本题考查了直线与平面平行、平面与平面平行的判定知识,熟练地掌握线面平行、面面平行的判定方法是解答本题的关键.

练习册系列答案
相关题目
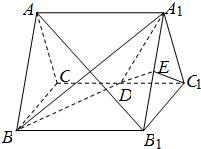 如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点. 如图,已知正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)异面直线AC与B1C1所成的角是
如图,已知正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)异面直线AC与B1C1所成的角是 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是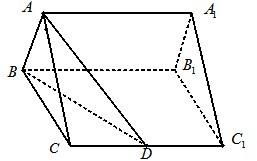 如图,已知正三棱柱ABC-A1B1C1的底面正三角形的边长是2,D是CC1的中点,直线AD与侧面BB1C1C所成的角是45°.
如图,已知正三棱柱ABC-A1B1C1的底面正三角形的边长是2,D是CC1的中点,直线AD与侧面BB1C1C所成的角是45°. 如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小是
如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,则异面直线AB1和A1C所成的角的余弦值大小是