题目内容
 如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,垂足分别是D、E,则以A、B为焦点且过D、E的椭圆与双曲线的离心率分别为e1,e2,则
如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,垂足分别是D、E,则以A、B为焦点且过D、E的椭圆与双曲线的离心率分别为e1,e2,则| 1 |
| e1 |
| 1 |
| e2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据题意设出AB,进而根据椭圆的定义可求得a和c的关系式,求得椭圆的离心率;利用双曲线的性质,求得a和c关系,求得双曲线的离心率,然后求得二者离心率倒数和.
解答:
解:设|AB|=2c,则在椭圆中,有c+
c=2a,
∴
=
=
,
而在双曲线中,有
c-c=2a,
∴
=
=
,
∴
+
=
+
=
.
故答案为:
.
| 3 |
∴
| 1 |
| e1 |
| a |
| c |
1+
| ||
| 2 |
而在双曲线中,有
| 3 |
∴
| 1 |
| e2 |
| a |
| c |
| ||
| 2 |
∴
| 1 |
| e1 |
| 1 |
| e2 |
1+
| ||
| 2 |
| ||
| 2 |
| 3 |
故答案为:
| 3 |
点评:题给出椭圆、双曲线满足的条件,求它们的离心率之和.着重考查了解直角三角形、椭圆和双曲线的定义与简单几何性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知点F是抛物线Γ:x2=2py(p>0)的焦点,点M(x0,1)到F的距离为2.
已知点F是抛物线Γ:x2=2py(p>0)的焦点,点M(x0,1)到F的距离为2.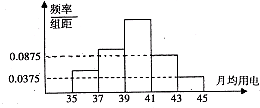 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图所示;其中直方图从左到右前3个小矩形的面积之比为1:2:3.该乡镇月均用电量在37~39之内的居民共有
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图所示;其中直方图从左到右前3个小矩形的面积之比为1:2:3.该乡镇月均用电量在37~39之内的居民共有