题目内容
已知函数f(x)=|log3x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m,n2]上的最大值为2,则m+n=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:先结合函数f(x)=|log3x|的图象和性质,再由f(m)=f(n),得到m,n的倒数关系,再由“若f(x)在区间[m,n2]上的最大值为2”,求得m、n的值,从而求得m+n的值.
解答:
解:∵f(x)=|log3x|,正实数m,n满足m<n,且f(m)=f(n),∴-log3m=log3n,∴mn=1.
∵f(x)在区间[m,n2]上的最大值为2,函数f(x)在[m,1)上是减函数,在(1,n2]上是增函数,
∴-log3m=2,或log3n2=2.
若-log3m=2,则m=3-2=
,故n=9,n2=81,故f(x)在区间[m,n2]上的最大值为log381=4,不满足条件.
若log3n2=2,则n=3,m=
,由于|log3m|=1<2,故满足f(x)在区间[m,n2]上的最大值为2,
综合可得 m=
,n=3,故n+m=
,
故选:D.
∵f(x)在区间[m,n2]上的最大值为2,函数f(x)在[m,1)上是减函数,在(1,n2]上是增函数,
∴-log3m=2,或log3n2=2.
若-log3m=2,则m=3-2=
| 1 |
| 9 |
若log3n2=2,则n=3,m=
| 1 |
| 3 |
综合可得 m=
| 1 |
| 3 |
| 10 |
| 3 |
故选:D.
点评:本题主要考查对数函数的图象和性质,特别是取绝对值后考查的特别多,解决的方法多数用数形结合法,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
执行如图所示的程序框图,输出的S值为( )


| A、250-1 | ||
| B、251-1 | ||
C、
| ||
D、
|
已知斜率为-
的直线与椭圆
+
=1,(a>b>0)交于两点,若这两点在x轴的射影恰好是椭圆的焦点,则e为( )
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC中,∠BAC=120°,AB=2,AC=1,D是边BC上的一点(包括端点),则
•
的取值范围是( )
| AD |
| BC |
| A、[1,2] |
| B、[0,1] |
| C、[0,2] |
| D、[-5,2] |
 如图,在平行四边形ABCD中,O是对角线AC、BD的交点,N是线段OD的中点,AN的延长线于CD交于点E,则下列说法错误的是( )
如图,在平行四边形ABCD中,O是对角线AC、BD的交点,N是线段OD的中点,AN的延长线于CD交于点E,则下列说法错误的是( )A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
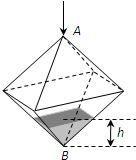 如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )
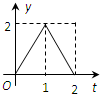
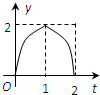
如图所示,连结棱长为2cm的正方体各面的中心得一个多面体容器,从顶点A处向该容器内注水,注满为止.已知顶点B到水面的高度h以每秒1cm匀速上升,记该容器内水的体积V(cm3)与时间T(S)的函数关系是V(t),则函数V(t)的导函数y=V′(t)的图象大致是( )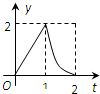
 如图,以椭圆C:
如图,以椭圆C: