题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() .
.
(1)证明: ![]() ;
;
(2)若当![]() 时,
时, 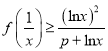 ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据导数几何意义得切线斜率为![]() ,再根据切线过点
,再根据切线过点![]() ,解得
,解得![]() 导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为
导数可得导函数零点,列表分析导函数符号变号规律可得函数单调性,根据函数单调性可得函数最小值为0,即得结论,(2)先化简不等式为![]() ,分离得
,分离得![]() ,再利用导数求函数
,再利用导数求函数![]() 单调性,利用罗伯特法则求最大值,即得
单调性,利用罗伯特法则求最大值,即得![]() 的取值范围.
的取值范围.
试题解析:(1)曲线![]() 在
在![]() 处的切线为
处的切线为![]() ,即
,即![]()
由题意得![]() ,解得
,解得![]()
所以![]()
从而![]()
因为当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在区间
在区间![]() 上是减函数,区间
上是减函数,区间![]() 上是增函数,
上是增函数,
从而![]() .
.
(2)由题意知,当![]() 时,
时, ![]() ,所以
,所以![]()
从而当![]() 时,
时, ![]() ,
,
由题意知 ,即
,即![]() ,其中
,其中![]()
设![]() ,其中
,其中![]()
设![]() ,即
,即![]() ,其中
,其中![]()
则![]() ,其中
,其中![]()
(1)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是增函数
是增函数
从而当![]() 时,
时, ![]() ,
,
所以![]() 是增函数,从而
是增函数,从而![]() .
.
故当![]() 时符合题意.
时符合题意.
(2)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,
,
所以![]() 在区间
在区间![]() 上是减函数
上是减函数
从而当![]() 时,
时, ![]()
所以![]() 在
在![]() 上是减函数,从而
上是减函数,从而![]()
故当![]() 时不符合题意.
时不符合题意.
(3)当![]() 时,因为
时,因为![]() 时,
时, ![]() ,所以
,所以![]() 是减函数
是减函数
从而当![]() 时,
时, ![]()
所以![]() 是减函数,从而
是减函数,从而![]()
故当![]() 时不符合题意
时不符合题意
综上![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
22
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
【答案】(1) ![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的极坐标方程为
的极坐标方程为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先根据三角函数平方关系消参数得曲线![]() ,再根据
,再根据![]() 将曲线
将曲线![]() 的
的![]() 极坐标方程;(2)将
极坐标方程;(2)将![]() 代人曲线
代人曲线![]() 的极坐标方程,再根据
的极坐标方程,再根据![]() 求
求![]() .
.
试题解析:(1)曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)
为参数)
可化为普通方程![]() ,
,
由![]() ,可得曲线
,可得曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径为
的极径为![]() ,
,
射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径满足
的极径满足![]() ,解得
,解得![]() ,
,
所以![]() .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表如下,频率分布直方图如图:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率.


