题目内容
若b>a>0,满足tanα=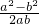 ,且sinα=
,且sinα=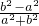 的角α的集合是
的角α的集合是
- A.{α|0<α<
 }
} - B.{α|
 +2kπ≤α≤π+2kπ,k∈Z}
+2kπ≤α≤π+2kπ,k∈Z} - C.{α|2kπ≤α≤π+2kπ,k∈Z}
- D.{α|
 +2kπ<α<π+2kπ,k∈Z}
+2kπ<α<π+2kπ,k∈Z}
D
分析:根据已知sinα和tanα 的关系求出cosα的表达式,然后根据b>a>0依次判断cosα和sinα的范围,最后根据正弦函数和余弦函数的图象得出结果
解答:∵
∴
∵b>a>0
∴a2+b2>2ab
∴
即:-1<cosα<0 ①
而根据b>a>0,
sinα=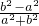 >0 ②
>0 ②
根据①②可得:
{α| +2kπ<α<π+2kπ,k∈Z}
+2kπ<α<π+2kπ,k∈Z}
故答案为D
点评:本题考查正弦余弦函数的图象,其中涉及到了正弦函数余弦函数与正切的关系,属于中档题
分析:根据已知sinα和tanα 的关系求出cosα的表达式,然后根据b>a>0依次判断cosα和sinα的范围,最后根据正弦函数和余弦函数的图象得出结果
解答:∵

∴

∵b>a>0
∴a2+b2>2ab
∴

即:-1<cosα<0 ①
而根据b>a>0,
sinα=
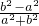 >0 ②
>0 ②根据①②可得:
{α|
 +2kπ<α<π+2kπ,k∈Z}
+2kπ<α<π+2kπ,k∈Z}故答案为D
点评:本题考查正弦余弦函数的图象,其中涉及到了正弦函数余弦函数与正切的关系,属于中档题

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 (2010•重庆三模)如图,已知圆G:
(2010•重庆三模)如图,已知圆G: