题目内容

函数y=5
x-4
+12
5-x
的最大值是
13
13
．
分析：由函数解析式求出函数的定义域，再利用柯西不等式，即可得到结论．
解答：解：由柯西不等式得，
y=5
x-4
+12
5-x
≤
52+122
x-4+5-x
=13，
当且仅当5
x-4
=12
5-x
时取等号，
此时函数取得最大值为 13．
故答案为：13．
点评：本题考查了柯西不等式求函数最值，关键是对所给函数解析式灵活变形，再应用柯西不等式，此类型是函数中两个根式变量的系数不互为相反数（互为相反数时可用基本不等式），但是符号相反，注意先求函数的定义域，验证等号成立的条件．
练习册系列答案
相关题目
已知函数f(x)=
a
3
x3-
a+1
2
x2+x+b，其中a，b∈R．
（Ⅰ）若曲线y=f（x）在点P（2，f（2））处的切线方程为y=5x-4，求函数f（x）的解析式；
（Ⅱ）当0＜a≠1时，讨论函数f（x）的单调性．
函数y=log（1-x）（5x-4）的定义域是（　　）
已知函数f(x)=
a
3
x3-
a+1
2
x2+x+b，其中a，b∈R．
（1）若曲线y=f（x）在点P（2，f（2））处的切线方程为y=5x-4，求函数f（x）的解析式；
（2）当a＞0且a≠0时，讨论函数f（x）的单调性；
（3）当a=3时，若方程f（x）=0有三个根，求b的取值范围．
下列说法正确的有（　　）
①集合A={x∈z|x=2k+1，k∈z}与集合B={x|x=2k-1，k∈z}是相等集合；②设集合A={x|（x-3）（x-a）=0，a∈R}，B={x|x2-5x+4=0}，则A∪B={1，3，4，a}；③函数y=
x+1
x-1
在区间[2，6]上的最大值为3；④函数y=
1
x2
在定义域上是减函数．
有下列四个命题：①函数y=2x(x∈N)的图象是一条直线;②函数y=5x(x∈{1,2,3,4})，不能用列表法表示;

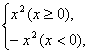③函数y=,的图象是抛物线;④设正三角形的边长为x，面积为y，则面积函数的解析法表示为y=x2(x＞0).其中正确命题的个数是（    ）

A.1                B.2                C.3              D.4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网