题目内容
()如图,四棱锥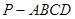 中,
中,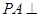 平面
平面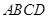 ,底面
,底面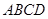 是平行四边形,
是平行四边形,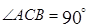 ,
,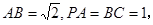
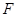 是
是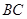 的中点
的中点

(Ⅰ)求证: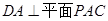
(Ⅱ)试在线段 上确定一点
上确定一点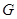 ,使
,使 ,求三棱锥
,求三棱锥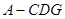 的体积.
的体积.
【答案】
(Ⅰ)详见解析;(Ⅱ)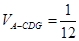 .
.
【解析】
试题分析:(Ⅰ)求证: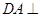 平面
平面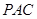 ,先证明线线垂直,即证
,先证明线线垂直,即证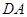 垂直平面
垂直平面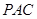 内的两条相交直线即可,由题意
内的两条相交直线即可,由题意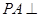 平面
平面 ,即
,即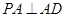 ,在平面
,在平面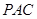 内再找一条垂线即可,由已知
内再找一条垂线即可,由已知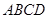 是平行四边形,
是平行四边形,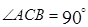 ,从而可得
,从而可得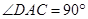 ,即
,即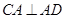 ,从而可证
,从而可证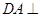 平面
平面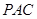 ;(Ⅱ)试在线段
;(Ⅱ)试在线段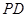 上确定一点
上确定一点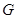 ,使
,使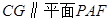 ,求三棱锥
,求三棱锥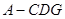 的体积,注意到
的体积,注意到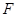 是
是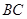 的中点,可取
的中点,可取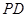 的中点为
的中点为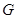 ,在平面
,在平面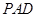 内作
内作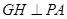 于
于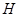 ,则四边形
,则四边形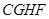 为平行四边形,
为平行四边形,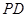 的中点
的中点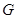 即为所确定的点,求三棱锥
即为所确定的点,求三棱锥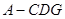 的体积,可转化为求三棱锥
的体积,可转化为求三棱锥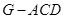 的体积,由题意容易求得,从而得解.
的体积,由题意容易求得,从而得解.
试题解析:(Ⅰ)∵四边形ABCD是平行四边形,∠ACB=90°,∴∠DAC=90°
∵PA⊥平面ABCD,DAÌ平面ABCD,∴PA⊥DA,又∵AC⊥DA,AC∩PA=A,∴DA⊥平面PAC (6分)
(Ⅱ)设PD的中点为G,在平面PAD内作GH⊥PA于H,
则GH平行且等于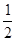 AD.
(8分)
AD.
(8分)
连接FH,则四边形FCGH为平行四边形,∴GC∥FH,∵FHÌ平面PAE,CGË平面PAE,
∴GC∥平面PAE,∴G为PD中点时,GC∥平面PAE. (10分)
设S为AD的中点,连结GS,则GS平行且等于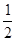 PA=
PA=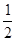
∵PA⊥平面ABCD,∴GS⊥平面ABCD.
∴VA-CDG=VG-ACD=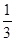 S△ACD·GS=
S△ACD·GS=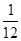 .
(12分)
.
(12分)
考点:线面垂直的判断,求几何体的体积.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,四棱锥中,底面ABCD是菱形,SA=SD=
如图,四棱锥中,底面ABCD是菱形,SA=SD= (2011•聊城一模)如图,四棱锥中S-ABCD中,底面ABCD是棱形,其对角线的交点为O,且SA=AC,SA⊥BD,
(2011•聊城一模)如图,四棱锥中S-ABCD中,底面ABCD是棱形,其对角线的交点为O,且SA=AC,SA⊥BD,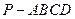 中,
中,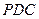 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是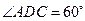 的菱形,
的菱形,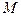 为
为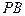 的中点.
的中点.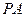 与底面
与底面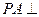 平面
平面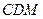 ;
;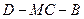 的余弦值.
的余弦值. 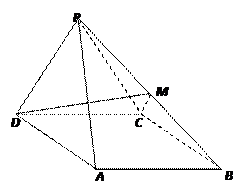
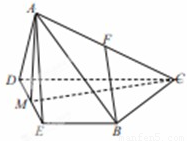
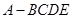 中,侧面
中,侧面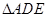 是等边三角形,在底面等腰梯形
是等边三角形,在底面等腰梯形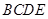 中,
中,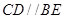 ,
,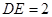 ,
,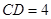 ,
,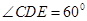 ,
,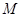 为
为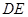 的中点,
的中点,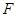 为
为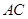 的中点,
的中点,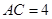 .
.
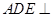 平面
平面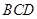 ;
;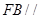 平面
平面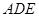 .
.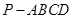 中,
中,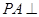 平面
平面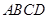 ,四边形
,四边形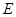 ,
,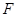 分别是
分别是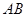 ,
,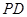 的中点.若
的中点.若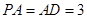 ,
,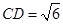 。
。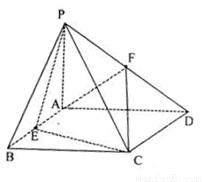
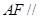 平面
平面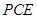 ;
;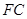 平面
平面